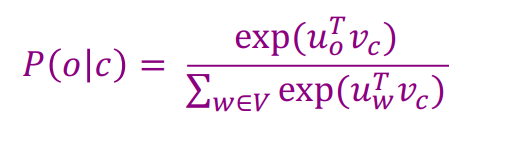在所有的NLP任务中,首先面临的第一个问题是我们该如何表示单词。这种表示将作为inputs输入到特定任务的模型中,如机器翻译,文本分类等典型NLP任务。
一个很容易想到的解决方案是使用同义词来表示一个单词的意义。 比如WordNet,一个包含同义词(和有“is a”关系的词)的词库。
导包
!pip install --user -U nltk!python -m nltk.downloader popular如获取"good"的同义词
from nltk.corpus import wordnet as wn
poses = { 'n':'noun', 'v':'verb', 's':'adj (s)', 'a':'adj', 'r':'adv'}
for synset in wn.synsets("good"):
print("{}: {}".format(poses[synset.pos()],", ".join([l.name() for l in synset.lemmas()])))如获取与“pandas”有"is a"关系的词
panda = wn.synset("panda.n.01")
hyper = lambda s: s.hypernyms()
list(panda.closure(hyper))WordNet的问题
- 单词与单词之间缺少些微差异的描述。比如“高效”只在某些语境下是"好"的同义词
- 丢失一些词的新含义。比如“芜湖”,“蚌埠”等词的新含义
- 相对主观
- 需要人手动创建和调整
- 无法准确计算单词的相似性
在传统NLP中,人们使用one-hot向量(一个向量只有一个值为1,其余的值为0)来表示单词
如:motel = [0 0 0 0 0 0 0 0 0 0 1 0 0 0 0]
如:hotel = [0 0 0 0 0 0 0 1 0 0 0 0 0 0 0]
one-hot向量的维度是词汇表的大小(如:500,000)
注:上面示例词向量的维度为方便展示所以比较小
one-hot向量表示单词的问题:
- 这些词向量是正交向量,无法通过数学计算(如点积)计算相似性
- 依赖WordNet等同义词库建立相似性效果也不好
如果我们可以使用某种方法为每个单词构建一个合适的dense vector,如下图,那么通过点积等数学计算就可以获得单词之间的某种联系
首先,我们引入一个上世纪五十年代,一个语言学家的研究成果:“一个单词的意义由它周围的单词决定”
“You shall know a word by the company it keeps” (J. R. Firth 1957: 11)
这是现代NLP中一个最为成功的理念。
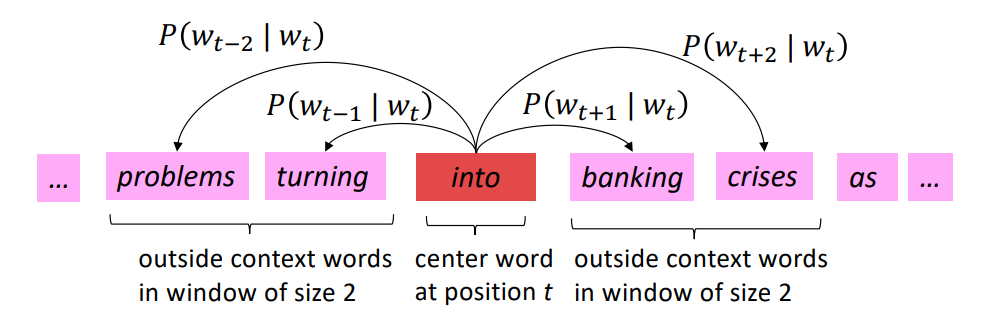
我们先引入上下文context的概念:当单词 w 出现在文本中时,其上下文context是出现在w附近的一组单词(在固定大小的窗口内),如下图
这些上下文单词context words决定了banking的意义
Word2vec(Mikolov et al. 2013)是一个用来学习dense word vector的算法:
- 我们使用大量的文本语料库
- 词汇表中的每个单词都由一个词向量dense word vector表示
- 遍历文本中的每个位置 t,都有一个中心词 c(center) 和上下文词 o(“outside”),如图1中的banking
- 在整个语料库上使用数学方法最大化单词o在单词c周围出现了这一事实,从而得到单词表中每一个单词的dense vector
- 不断调整词向量dense word vector以达到最好的效果
Word2vec包含两个模型,Skip-gram与CBOW。下面,我们先讲Skip-gram模型,用此模型详细讲解概述中所提到的内容。
概述中我们提到,我们希望最大化单词o在单词c周围出现了这一事实,而我们需要用数学语言表示“单词o在单词c周围出现了”这一事件,如此才能进行词向量的不断调整。
很自然地,我们需要使用概率工具描述事件的发生,我们想到用条件概率$P(o|c)$表示“给定中心词c,它的上下文词o在它周围出现了”
下图展示了以“into”为中心词,窗口大小为2的情况下它的上下文词。以及相对应的$P(o|c)$
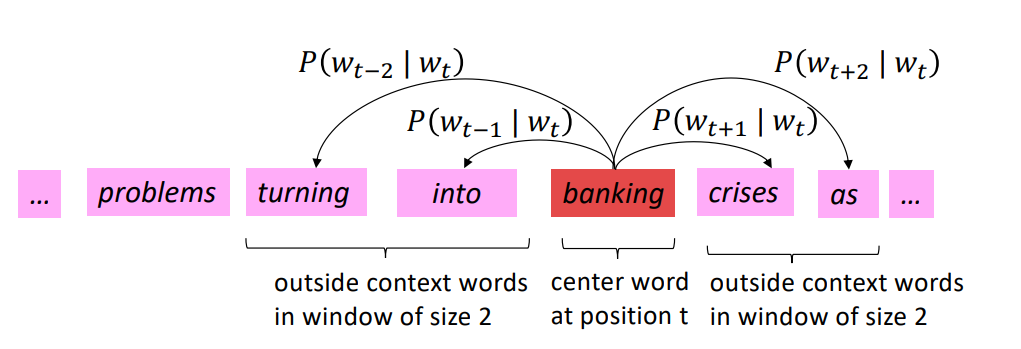
我们滑动窗口,再以banking为中心词
那么,如果我们在整个语料库上不断地滑动窗口,我们可以得到所有位置的$P(o|c)$,我们希望在所有位置上最大化单词o在单词c周围出现了这一事实,由极大似然法,可得:
此式还可以依图3写为:
加log,加负号,缩放大小可得:
上式即为skip-gram的损失函数,最小化损失函数,就可以得到合适的词向量
得到式1后,产生了两个问题:
-
P(o|c)怎么表示?
-
为何最小化损失函数能够得到良好表示的词向量dense word vector?
回答1:我们使用中心词c和上下文词o的相似性来计算$P(o|c)$,更具体地,相似性由词向量的点积表示:$u_o \cdot v_c$。
使用词向量的点积表示P(o|c)的原因:1.计算简单 2.出现在一起的词向量意义相关,则希望它们相似
又P(o|c)是一个概率,所以我们在整个语料库上使用softmax将点积的值映射到概率,如图6
注:注意到上图,中心词词向量为$v_{c}$,而上下文词词向量为$u_{o}$。也就是说每个词会对应两个词向量,在词w做中心词时,使用$v_{w}$作为词向量,而在它做上下文词时,使用$u_{w}$作为词向量。这样做的原因是为了求导等操作时计算上的简便。当整个模型训练完成后,我们既可以使用$v_{w}$作为词w的词向量,也可以使用$u_{w}$作为词w的词向量,亦或是将二者平均。在下一部分的模型结构中,我们将更清楚地看到两个词向量究竟在模型的哪个位置。
回答2:由上文所述,$P(o|c)=softmax(u_{o^T} \cdot v_c)$。所以损失函数是关于$u_{o}$和$v_c$的函数,我们通过梯度下降法调整$u_{o}$和$v_c$的值,最小化损失函数,即得到了良好表示的词向量。
如图八所示,这是一个输入为1 X V维的one-hot向量(V为整个词汇表的长度,这个向量只有一个1值,其余为0值表示一个词),单隐藏层(隐藏层的维度为N,这里是一个超参数,这个参数由我们定义,也就是词向量的维度),输出为1 X V维的softmax层的模型。
模型的输入为1 X V形状的one-hot向量(V为整个词汇表的长度,这个向量只有一个1值,其余为0值表示一个词)。隐藏层的维度为N,这里是一个超参数,这个参数由我们定义,也就是词向量的维度。$W^{I}$为V X N的参数矩阵。
我们这里,考虑Skip-gram算法,输入为中心词c的one-hot表示
由输入层到隐藏层,根据矩阵乘法规则,可知,
而$W^{O}$中的每一列即为词汇表中的每一个单词的词向量u。根据乘法规则,1 X N 的隐藏层乘上N X V的$W^{O}$参数矩阵,得到的1 X V 的输出层的每一个值即为$u_{w^T} \cdot v_c$,加上softmax变化即为$P(w|c)$。
有V个w,其中的P(o|c)即实际样本中的上下文词的概率,为我们最为关注的值。
如上文所述,Skip-gram为给定中心词,预测周围的词,即求P(o|c),如下图所示:
而CBOW为给定周围的词,预测中心词,即求P(c|o),如下图所示:
注意:在使用CBOW时,上文所给出的模型结构并没有变,在这里,我们输入多个上下文词o,在隐藏层,将这多个上下文词经过第一个参数矩阵的计算得到的词向量相加作为隐藏单元的值。其余均不变,$W^{O}$中的每一列依然为为词汇表中的每一个单词的词向量u。
我们再看一眼,通过softmax得到的$P(o|c)$,如图:
可以看到,$P(o|c)$的分母需要在整个单词表上做乘积和exp运算,这无疑是非常消耗计算资源的,Word2vec的作者针对这个问题,做出了改进。
他提出了两种改进的方法:Hierarchical Softmax和Negative Sampling,因为Negative Sampling更加常见,所以我们下面只介绍Negative Sampling,感兴趣的朋友可以在文章下面的参考资料中学习Hierarchical Softmax。
我们依然以Skip-gram为例(CBOW与之差别不大,感兴趣的朋友们依然可以参阅参考资料)
我们首先给出负采样的损失函数:
其中$\sigma$为sigmoid函数$1/(1+e^{-x})$,
由函数单调性易知,
损失函数关于$v_c$的导数:
可以看到涉及整个U矩阵的计算,计算量很大,关于$u_w$的导数读者可自行推导
损失函数及其梯度的求解
来自:https://github.com/lrs1353281004/CS224n_winter2019_notes_and_assignments
def naiveSoftmaxLossAndGradient(
centerWordVec,
outsideWordIdx,
outsideVectors,
dataset
):
""" Naive Softmax loss & gradient function for word2vec models
Arguments:
centerWordVec -- numpy ndarray, center word's embedding
in shape (word vector length, )
(v_c in the pdf handout)
outsideWordIdx -- integer, the index of the outside word
(o of u_o in the pdf handout)
outsideVectors -- outside vectors is
in shape (num words in vocab, word vector length)
for all words in vocab (tranpose of U in the pdf handout)
dataset -- needed for negative sampling, unused here.
Return:
loss -- naive softmax loss
gradCenterVec -- the gradient with respect to the center word vector
in shape (word vector length, )
(dJ / dv_c in the pdf handout)
gradOutsideVecs -- the gradient with respect to all the outside word vectors
in shape (num words in vocab, word vector length)
(dJ / dU)
"""
# centerWordVec: (embedding_dim,1)
# outsideVectors: (vocab_size,embedding_dim)
scores = np.matmul(outsideVectors, centerWordVec) # size=(vocab_size, 1)
probs = softmax(scores) # size=(vocab, 1)
loss = -np.log(probs[outsideWordIdx]) # scalar
dscores = probs.copy() # size=(vocab, 1)
dscores[outsideWordIdx] = dscores[outsideWordIdx] - 1 # dscores=y_hat - y
gradCenterVec = np.matmul(outsideVectors, dscores) # J关于vc的偏导数公式 size=(vocab_size, 1)
gradOutsideVecs = np.outer(dscores, centerWordVec) # J关于u的偏导数公式 size=(vocab_size, embedding_dim)
return loss, gradCenterVec, gradOutsideVecs负采样损失函数关于$v_c$的导数:
可以看到其只与$u_k$和$u_o$有关,避免了在整个单词表上的计算
负采样方法的损失函数及其导数的求解
def negSamplingLossAndGradient(
centerWordVec,
outsideWordIdx,
outsideVectors,
dataset,
K=10
):
negSampleWordIndices = getNegativeSamples(outsideWordIdx, dataset, K)
indices = [outsideWordIdx] + negSampleWordIndices
gradCenterVec =np.zeros(centerWordVec.shape) # (embedding_size,1)
gradOutsideVecs = np.zeros(outsideVectors.shape) # (vocab_size, embedding_size)
loss = 0.0
u_o = outsideVectors[outsideWordIdx] # size=(embedding_size,1)
z = sigmoid(np.dot(u_o, centerWordVec)) # size=(1, )
loss -= np.log(z) # 损失函数的第一部分
gradCenterVec += u_o * (z - 1) # J关于vc的偏导数的第一部分
gradOutsideVecs[outsideWordIdx] = centerWordVec * (z - 1) # J关于u_o的偏导数计算
for i in range(K):
neg_id = indices[1 + i]
u_k = outsideVectors[neg_id]
z = sigmoid(-np.dot(u_k, centerWordVec))
loss -= np.log(z)
gradCenterVec += u_k * (1-z)
gradOutsideVecs[neg_id] += centerWordVec * (1 - z)
return loss, gradCenterVec, gradOutsideVecs参考资料
- Mikolov T, Sutskever I, Chen K, et al. Distributed representations of words and phrases and their compositionality[J]. Advances in neural information processing systems, 2013, 26.
- https://www.cnblogs.com/peghoty/p/3857839.html
- http://web.stanford.edu/class/cs224n/