原始 Markdown文档、Visio流程图、XMind思维导图见：https://github.com/LiZhengXiao99/Navigation-Learning

[TOC]

一、OB-GINS 简介

1、程序概述

基于图优化的 IMU/GNSS 松组合解算，其 IMU 预积分算法相比以视觉为主的 ORB-SLAM3、VINS 要精细一些，

代码总共 2100+ 行，适合作为学习图优化、IMU 预积分的入门代码。

开源地址：https://github.com/i2Nav-WHU/OB_GINS，

支持四种预积分模式：

2、相关论文

Impact of the Earth Rotation Compensation on MEMS-IMU Preintegration of Factor Graph Optimization，下载
摘要翻译：
- 在基于滤波的 GNSS/INS 组合导航系统中，精密的 IMU 机械编排需要考虑到地球自转、牵连角速度、科氏加速度等的影响；然而大多数的图优化框架中的 IMU 预积分模型都没有考虑这些因素。
- 我们提出了一种进行了地球自转补偿的滑动窗口图优化 GNSS/INS 组合导航算法，并且评估了地球自转等对 MEMS-IMU 预积分的影响。
- 测试了 GNSS 量测缺失，采用了有效的方法对预积分结果进行评价。结果表明，此方法预积分的精度与精密机械编排的精度相当；相比之下，IMU 在不补偿地球自转的情况下，预积分的精度显著低于机械编排的精度，有显著的精度降级。
- 当 GNSS 中断时间为 60 秒时，工业级 MEMS 的降级可能为 200% 模块，消费级 MEMS 芯片超过 10%。此外，如果 GNSS 中断时间更长，精度降级还会更显著。
Improved IMU Preintegration with Gravity Change and Earth Rotation for Optimization-Based GNSS/VINS，下载
摘要翻译：
- IMU 预积分技术广泛用于图优化框架的多源融合定位解算中，它可以避免高频率的 IMU 量测数据在迭代计算中重复积分，并且在偏差估计发生变化时保持偏差校正的能力。
- 自从 IMU 预积分被提出后，陆续有一些改变姿态参数和数值积分方法增强版本的算法被设计出来，然而这些版本都没有考虑到重力和地球自转。
- 在本文提出的算法中，我们利用了基于大地经纬高算出的重力向量，且预积分 IMU 测量的不确定性没有使用协方差矩阵，而是以平方根信息矩阵（SRIM）的形式传播，以获得更好的数值稳定性，并且易于在基于优化的框架中使用。
- 为了评估算法的精度，我们使用了两种级别的 IMU 数据进行测试，测试结果表明，改进的IMU预集成算法能够很好地应对重力变化和地球自转。当处理能有效感知地球自转的高级 IMU 的数据时，必须考虑地球自转。
- 如果忽略重力的变化，水平姿态的均方根误差（RMSE）大约是 1.38 倍的大地位移；此外，定位 RMSE 也不在有限的范围内；这意味着几十公里和几百米的实验中分别使用的低级别和高级 IMU。
GNSS/IMU/ODO/LiDAR-SLAM Integrated Navigation System Using IMU/ODO Pre-Integration，下载
摘要翻译：
- 在本文，我们提出一套 GNSS/IMU/ODO/Lidar-SLAM 融合导航定位算法。
- 前端进行航位推算，进行 IMU/ODO 预积分。后端通过图优化对 GNSS 坐标、IMU/ODO 预积分结果、LiDAR-SLAM 得出的相对位置和姿态进行融合。
- 里程计信息用于降低 IMU 预积分算法中的漂移率。滑动窗口算法可以通过减少图优化的参数，来降低图优化的计算量。
- 分别在露天区域和隧道情况下进行车辆数据测试；测试结果表明，所提出的导航系统可以有效地提高导航的精确度和鲁棒性。
- 在模拟两分钟 GNSS 中断期间，相比传统的 GNSS/INS/ODO组合算法，北东地的 RMS 分别下降 62.8%、72.3%、52.1%。此外，与 GNSS/IMU/Lidar-SLAM 组合相比，误差降低了 62.1% ，里程计和非完整约束的辅助下减少垂直误差为 72.3%。
- 在实际隧道案例中的测试表明，在弱环境特征区域激光雷达 SLAM 几乎不能工作，里程计在预集成中的辅助作用至关重要，并且可以有效地减少沿正向方向的定位漂移并保持 SLAM 短期内有效。
- 因此，提出的 GNSS/IMU/ODO/Lidar-SLAM 组合导航系统可以有效地融合来自多个来源的信息，以维护 SLAM 过程显著降低导航误差，尤其是在 GNSS 信号严重的恶劣地区退化和环境特征不足以用于激光雷达 SLAM。

Impact of the Earth Rotation Compensation on MEMS-IMU Preintegration of Factor Graph Optimization

3、代码分析

用 cloc 对 src 目录下 factors、fileio、preintegration 进行统计，结果如下：

4、第三方库

5、重点函数

主函数：

6、执行流程

二、编译、调试

三、类型定义

四、主函数

1、函数调用关系图

2、执行流程图

3、读取配置文件

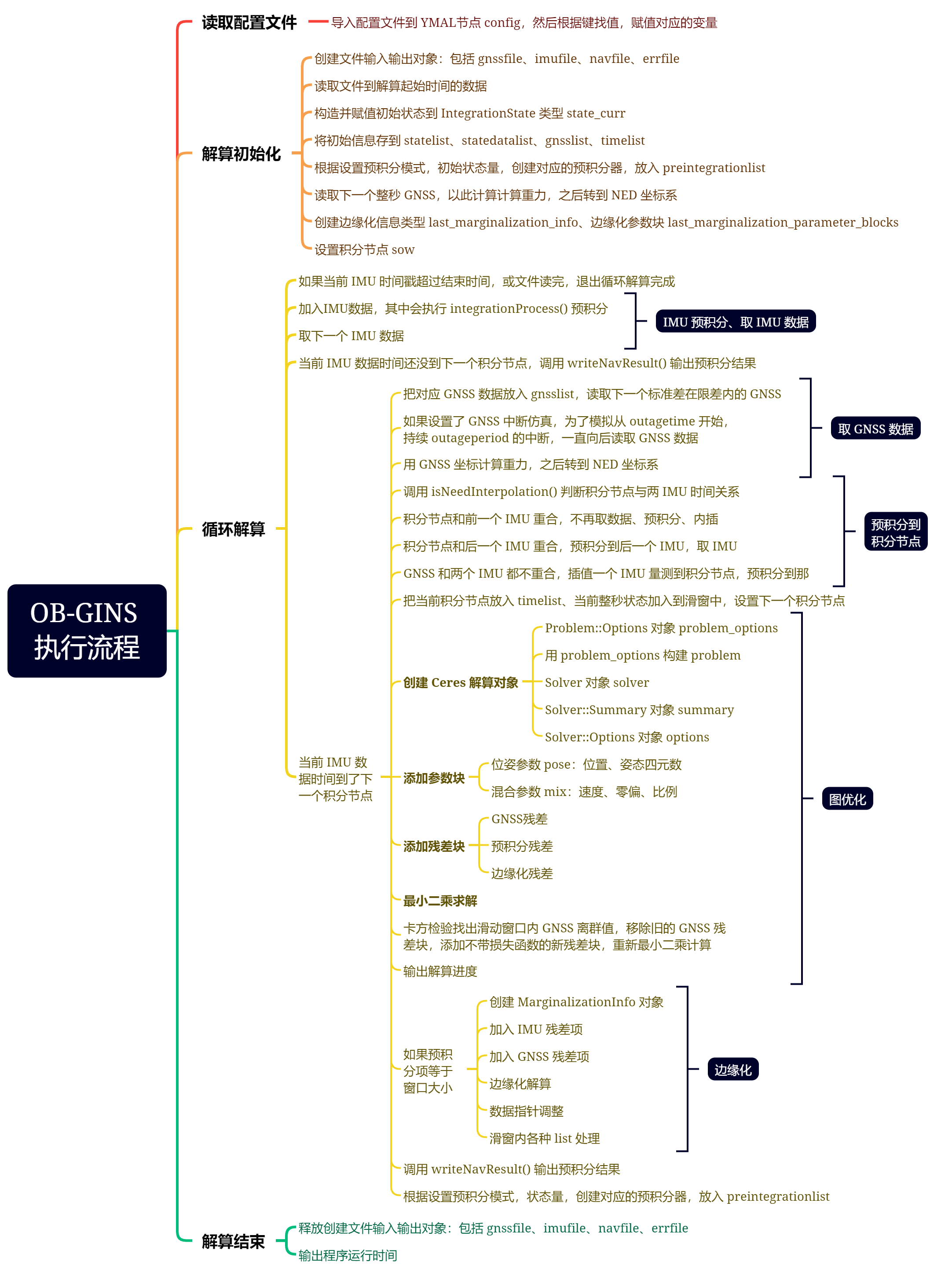
OB-GINS 主函数很长，可以说看懂主函数就把整个程序都看懂了，将近 500 行，可以分为三部分：

while 循环解算前：读取配置文件、创建解算对象，赋值初始的状态量，进行一次初始预积分。
while 循环解算：
while 循环解算后：释放创建的对象，输出解算时间。

判断参数数量，如果不为 2，说明没传入配置文件，提醒用户传配置文件路径，然后退出程序。输出程序信息，记录开始时间。

if (argc != 2) {
    std::cout << "usage: ob_gins ob_gins.yaml" << std::endl;
    return -1;
}

std::cout << "\nOB_GINS: An Optimization-Based GNSS/INS Integrated Navigation System\n\n";

auto ts = absl::Now();

导入配置选项

// 读取配置
// load configuration
YAML::Node config;
std::vector<double> vec;
try {
    config = YAML::LoadFile(argv[1]);
} catch (YAML::Exception &exception) {
    std::cout << "Failed to read configuration file" << std::endl;
    return -1;
}

// 时间信息
// processing time
int windows   = config["windows"].as<int>();
int starttime = config["starttime"].as<int>();
int endtime   = config["endtime"].as<int>();

// 迭代次数
// number of iterations
int num_iterations = config["num_iterations"].as<int>();

// 进行GNSS粗差检测
// Do GNSS outlier culling
bool is_outlier_culling = config["is_outlier_culling"].as<bool>();

// 初始化信息
// initialization
vec = config["initvel"].as<std::vector<double>>();
Vector3d initvel(vec.data());
vec = config["initatt"].as<std::vector<double>>();
Vector3d initatt(vec.data());
initatt *= D2R;

vec = config["initgb"].as<std::vector<double>>();
Vector3d initbg(vec.data());
initbg *= D2R / 3600.0;
vec = config["initab"].as<std::vector<double>>();
Vector3d initba(vec.data());
initba *= 1.0e-5;

// 数据文件
// data file
std::string gnsspath   = config["gnssfile"].as<std::string>();
std::string imupath    = config["imufile"].as<std::string>();
std::string outputpath = config["outputpath"].as<std::string>();
int imudatalen         = config["imudatalen"].as<int>();
int imudatarate        = config["imudatarate"].as<int>();

// 是否考虑地球自转
// consider the Earth's rotation
bool isearth = config["isearth"].as<bool>();

// 安装参数
// installation parameters
vec = config["antlever"].as<std::vector<double>>();
Vector3d antlever(vec.data());
vec = config["odolever"].as<std::vector<double>>();
Vector3d odolever(vec.data());
vec = config["bodyangle"].as<std::vector<double>>();
Vector3d bodyangle(vec.data());
bodyangle *= D2R;

// IMU噪声参数
// IMU noise parameters
auto parameters          = std::make_shared<IntegrationParameters>();
parameters->gyr_arw      = config["imumodel"]["arw"].as<double>() * D2R / 60.0;
parameters->gyr_bias_std = config["imumodel"]["gbstd"].as<double>() * D2R / 3600.0;
parameters->acc_vrw      = config["imumodel"]["vrw"].as<double>() / 60.0;
parameters->acc_bias_std = config["imumodel"]["abstd"].as<double>() * 1.0e-5;
parameters->corr_time    = config["imumodel"]["corrtime"].as<double>() * 3600;

bool isuseodo       = config["odometer"]["isuseodo"].as<bool>();
vec                 = config["odometer"]["std"].as<std::vector<double>>();
parameters->odo_std = Vector3d(vec.data());
parameters->odo_srw = config["odometer"]["srw"].as<double>() * 1e-6;
parameters->lodo    = odolever;
parameters->abv     = bodyangle;

// GNSS仿真中断配置
// GNSS outage parameters
bool isuseoutage = config["isuseoutage"].as<bool>();
int outagetime   = config["outagetime"].as<int>();
int outagelen    = config["outagelen"].as<int>();
int outageperiod = config["outageperiod"].as<int>();
auto gnssthreshold = config["gnssthreshold"].as<double>();

4、解算初始化

根据读进来的配置，构造解算用到的几个文件对象：

文件读取对象：gnssfile、imufile
构造输出文件对象：navfile、errfile

GnssFileLoader gnssfile(gnsspath);
ImuFileLoader imufile(imupath, imudatalen, imudatarate);
FileSaver navfile(outputpath + "/OB_GINS_TXT.nav", 11, FileSaver::TEXT);
FileSaver errfile(outputpath + "/OB_GINS_IMU_ERR.bin", 7, FileSaver::BINARY);
if (!imufile.isOpen() || !navfile.isOpen() || !navfile.isOpen() || !errfile.isOpen()) {
    std::cout << "Failed to open data file" << std::endl;
    return -1;
}

循环调用 imufile.next()、gnssfile.next() 读取 IMU、GNSS 数据，直到时间戳在解算时间范围内。循环结束后 imu_cur、gnss 分别存解算时间内第一个 IMU、GNSS 量测，且文件指针指向的位置也到达解算时间内数据的开头：

// 数据文件调整
// data alignment
IMU imu_cur, imu_pre;
do {
    imu_pre = imu_cur;
    imu_cur = imufile.next();
} while (imu_cur.time < starttime);

GNSS gnss;
do {
    gnss = gnssfile.next();
} while (gnss.time < starttime);

设置初始状态：

station_origin：

// 初始位置, 求相对
Vector3d station_origin = gnss.blh;
parameters->gravity     = Earth::gravity(gnss.blh);
gnss.blh                = Earth::global2local(station_origin, gnss.blh);

// 站心坐标系原点
parameters->station = station_origin;

std::vector<IntegrationState> statelist(windows + 1);
std::vector<IntegrationStateData> statedatalist(windows + 1);
std::deque<std::shared_ptr<PreintegrationBase>> preintegrationlist;
std::deque<GNSS> gnsslist;      // GNSS 数据双端对列
std::deque<double> timelist;    // 时间戳双端对列

Preintegration::PreintegrationOptions preintegration_options = Preintegration::getOptions(isuseodo, isearth);

// 赋值初始状态到 state_curr
// initialization
IntegrationState state_curr = {
    .time = round(gnss.time),
    .p    = gnss.blh - Rotation::euler2quaternion(initatt) * antlever,
    .q    = Rotation::euler2quaternion(initatt),
    .v    = initvel,
    .bg   = initbg,
    .ba   = initba,
    .sodo = 0.0,
    .abv  = {bodyangle[1], bodyangle[2]},
};
std::cout << "Initilization at " << gnss.time << " s " << std::endl;

statelist[0]     = state_curr;
statedatalist[0] = Preintegration::stateToData(state_curr, preintegration_options);
gnsslist.push_back(gnss);

double sow = round(gnss.time);
timelist.push_back(sow);

初始预积分，根据设置预积分模式，调用 createPreintegration() 创建对应的预积分器，放入 preintegrationlist：

preintegrationlist.emplace_back(
    Preintegration::createPreintegration(parameters, imu_pre, state_curr, preintegration_options));

5、循环解算

下面进入 while 循环解算，如果在解算时间内，且文件还有数据，调用 addNewImu() 加入IMU数据，其中会执行 integrationProcess() 预积分，然后再读取下一个 IMU 数据：

// 如果当前 IMU 时间戳超过结束时间，或文件读完，退出循环解算完成
if ((imu_cur.time > endtime) || imufile.isEof()) {
    break;
}

// 加入IMU数据，其中会执行 integrationProcess() 预积分
// Add new imu data to preintegration
preintegrationlist.back()->addNewImu(imu_cur);

imu_pre = imu_cur;
imu_cur = imufile.next();

判断读进来 IMU 时间是否等于设置的 GNSS 时间，不等于就直接调用 writeNavResult() 输出解算信息：

auto integration = *preintegrationlist.rbegin();
writeNavResult(integration->endTime(), station_origin, integration->currentState(), navfile, errfile);

6、解算结束

五、IMU 预积分

六、因子图优化

1、因子图模型

因子图作为一种数学工具，是用因子描述多变量复杂函数的二维图，经常被用于多源融合导航中。因子图优化就是将优化问题转换成图的形式，图由边和顶点组成。边连接着顶点，表示顶点之间的一种关系。顶点表估计问题中的未知随机变量，而因子表示有关这些变量的概率信息，从测量或先验信息中可以得出。

因子图是一种二分图模型，它表征了全局函数和局部函数之间的关系，同时也表示了各个变量与局部函数之间的关系，以下式为例： $$ {\begin{array}{l} g\left(x_{1}, x_{2}, x_{3}, x_{4}, x_{5}\right)=f_{A}\left(x_{1}\right) f_{B}\left(x_{2}\right) f_{C}\left(x_{1} x_{2} x_{3}\right) f_{D}\left(x_{3} x_{4}\right) f_{E}\left(x_{3} x_{5}\right) \end{array}} $$ 将全局函数 $g$ 转化为局部函数 $f$ 的乘积，其对应的因子图如下所示：

圆圈：每一个变量 $x$ 对应一个变量结点。
正方形：每一个局部函数 $f$ 对应一个因子结点。
线：当且仅当变量 $x$ 是局部函数 $f$ 的的自变量时，相应的变量节点和因子节点之间有一条边连接两个节点。

2、因子图优化状态估计模型

状态估计问题，就是是寻找 $X$ 来最好地描述观测值 $Z$。根据贝叶斯法则，状态量 $X$ 和观测量 $Z$ 的联合概率等于条件概率乘以边缘概率： $$ {P(X,Z) =P(Z \mid X) P(X)} $$ 式中：$P(Z|X)$ 为观测量 $Z$ 对应的概率；$P(X)$ 是状态量 $X$ 的先验概率。后验分布 $P(X|Z)$ 是一种常用且直观评估状态集和观测集之间拟合程度的方法，我们求解期望的状态集可以由通过后验分布的最大化来实现，也就是极大验后估计： $$ \hat{X}=\underset{X}{\arg \max } P(X \mid Z) $$

有些文章用极大似然估计来介绍因子图优化，都可以，极大后验估计是极大似然估计在包含了先验“量测”后的特例，就多源融合导航而言，这两种最优估计没有本质上的区别。

用极大似然估计来理解：就惯性/GNSS 融合导航而言，不同传感器之间的量测，以及同一传感器在不同时刻的量测都是独立的，因此全局似然函数可以因式分解成关于各独立量测的似然函数的乘积。

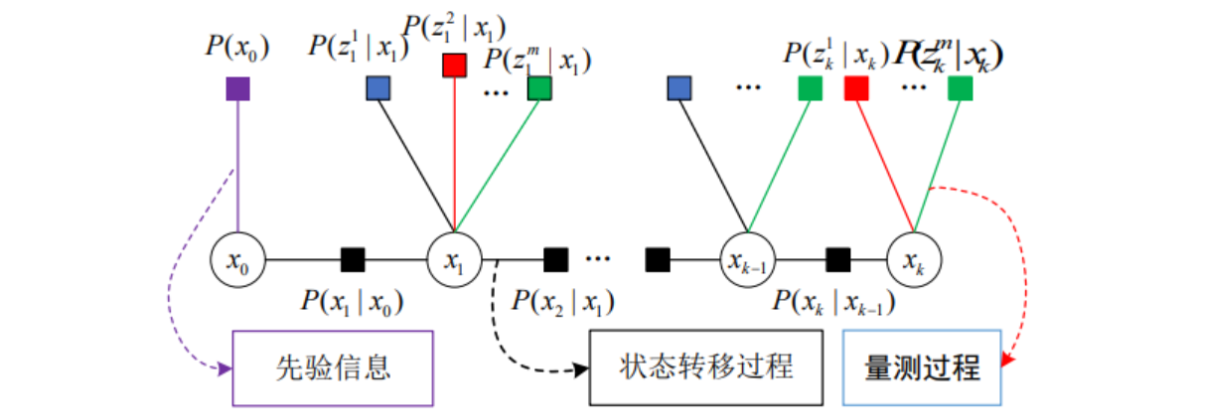
基于因子图的状态估计方法正是将状态估计理解为对系统联合概率密度函数的极大验后估计问题。一个系统可以描述为状态方程和量测方程两部分，并将状态误差和量测误差视为零均值白噪声即： $$ \left{\begin{array}{rr} x_{k}=f_{k}\left(x_{k-1}, u_{k}\right)+w_{k}, & w_{k} \sim N\left(0, \Sigma_{k}\right) \ z_{k}=h_{k}\left(x_{k}\right)+v_{k}, & v_{k} \sim N\left(0, \Lambda_{k}\right) \end{array}\right. $$ 根据正态分布的特性可以得到真实状态 $k_x$ 和理想量测 $k_z$ 的条件概率分布满足： $$ \left{\begin{array}{l} P\left(x_{k} \mid x_{k-1}\right) \propto e^{-\frac{1}{2}\left|f_{k}\left(x_{k-1}\right)-x_{k}\right|{\varepsilon{k}}^{2}} \ P\left(z_{k} \mid x_{k}\right) \propto e^{-\frac{1}{2} \mid f_{k}\left(x_{k}\right)-z_{k} |{k}^{2}} \end{array}\right. $$ 实际中的状态量 $X$ 往往是不知道的，而当前状态下的观测 $Z$ 是知道的，也就是 $P(Z|X)$ 是知道的，因此在因子图模型中： $$ X{k}^{}=\arg \max P\left(X_{k} \mid Z_{k}\right) \propto \arg \max P\left(X_{k}\right) P\left(Z_{k} \mid X_{k}\right) $$ 其中，$X_{k}=\left{x_{0: k}\right}$ 是状态的集合，$Z_{k}=\left{z_{0:k}^j\right}$ 是所有状态下量测的集合。若系统服从马尔科夫假设，那么： $$ \begin{aligned} X_{k}^{} & =\underset{X_{k}}{\arg \max } P\left(X_{k} \mid Z_{k}\right) \propto \underset{k}{\arg \max } P\left(x_{0}\right) \prod^{k}\left[P\left(x_{i} \mid x_{i-1}\right) \prod_{m_{i}}^{m_{i}}\left[P\left(z_{i}^{j} \mid x_{i}\right)\right]\right] \end{aligned} $$ 对式取对数得到后，将式代入式可以得到，系统的状态估计可等价为全局损失函数的联合优化： $$ X^{*}=\underset{X}{\arg\min } \sum_{i}^{k}\left{\left|f_{i}\left(x_{i-1}, u_{i}\right)-x_{i}\right|{\Sigma{i}}^{2}+\sum_{j=1}^{m_{j}}\left|h_{i}^{j}\left(x_{i}\right)-z_{i}^{j}\right|{\Lambda{i j}}^{2}\right} $$ 上式即为基于因子图优化的估计的一般表达式，其左项为系统状态转移过程，右项为量测过程，$\Sigma$ 和 $\Lambda$ 分别是状态转移过程和量测过程的协方矩阵，进行求解的是状态集合 X 。对于式，可以用下图进行表示：

圆圈：变量节点，表示系统待估计的状态，对应一个变量 $x$ 。
正方形：因子节点，表示先验信息、状态转移和量测过程，对应一个局部函数 $f$ ，其中：
- 紫色 $P(x_0)$ 为先验因子。
- 黑色 $P(x_1|x_0) \dots P(x_k|x_{k-1})$ 为状态转移，由上一时刻状态推测下一时刻状态。
- 其它为量测信息，$P(z|x)$ 表示在参数 $x$ 的条件下得到观测值 $z$。
线：当且仅当变量 $x$ 是局部函数 $f$ 的的自变量时，相应的变量节点和因子节点之间有一条边连接两个节点。
若在模型中加入其他传感器，只需将其添加到框架中相关的因子节点处即可。

利用因子图模型对估计系统的联合概率密度函数进行表示，可以直观地反映动态系统的动态演化过程和每个状态对应的量测过程。同时，图形化的表示使系统具有更好的通用性和扩展性。

3、因子图优化求解

每一个观测变量在上面贝叶斯网络里都是单独求解的（相互独立），所有的条件概率都是乘积的形式，且可分解，在因子图里面，分解的每一个项就是一个因子，乘积乘在一起用图的形式来描述就是因子图。整个因子图实际上就是每个因子单独的乘积。 求解因子图就是将这些因子乘起来，求一个最大值，得到的系统状态就是概率上最可能的系统状态。

先找到残差函数 $e(x)$，由因子节点可以得到我们估计的值和实际的测量值之间的差值，即每个因子 $f$ 会对应一个残差函数。根据中心极限定理，绝大多数传感器的噪声是符合高斯分布的，所以每个因子都是用高斯分布的指数函数来定义的。 $$ g(x)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right) $$ 指数函数对应了残差函数，包括两个部分：系统状态量和观测量。残差函数实际上表示的是用状态量去推测的观测量与实际观测量的区别。残差函数的表达式一般都是非线性的，可以通过改变变量 $X$ 来使残差函数最小化，残差函数最小，估计的值越符合观测值，套到因子图里面来看，因子图的求解是要所有因子的乘积最大化， $$ \hat{X}=\underset{X}{\arg \max } \prod_{i} \exp \left(-\frac{1}{2}\left|e_{i}(X i)\right|{\Sigma i}^{2}\right) $$ 对于负指数函数形式，每一个因子乘积最大化代表里面的 $e(x)$ 最小化，对目标函数取对数，概论问题转为非线性最小二乘问题： $$ \hat{X}=\underset{X}{\operatorname{arg} \operatorname{max}} \sum{i}\left(e_{\dot{\epsilon}}\left(x_{i}\right)\right)^{2} $$ 最优化问题可以选择高斯-牛顿法、列文博格-马夸尔特或者Dogleg等迭代优化算法求解，高斯-牛顿法比较简单，但稳定性较差，算法可能不收敛；列文博格-马夸尔特引入置信区间概念，约束下降的步长，提高稳定性，Dogleg也类似。**问题性质较好时可用高斯-牛顿法，问题条件恶劣时选择列文博格-马夸尔特或者Dogleg。**几种梯度下降方法比较如下：

最速梯度下降法：目标函数在 $x_k$ 处泰勒展开，保留一阶项，$x*= - J(x_k)$，最速下降法过于贪心，容易走出锯齿路线，反而增加迭代次数。
牛顿法：二阶泰勒展开，利用二次函数近似原函数。$H*X= - J$，牛顿法需要计算目标函数的海森矩阵阵，计算量大。规模较大时比较困难。
高斯-牛顿法（GN）：$f(x)$ 进行一阶泰勒展开，$f(x)$ 而不是 $F(x)$ ，高斯牛顿法用雅各比矩阵 $JJ^T$ 来作为牛顿法中二阶海森阵的近似，$HX=g$，在使用高斯牛顿法时，可能出现 $JJ^T$ 为奇异矩阵或者病态的情况，此时增量稳定性较差，导致算法不收敛。
列文伯格–马夸尔特方法（LM）：基于信赖区域理论，是由于高斯—牛顿方法在计算时需要保证矩阵的正定性，于是引入了一个约束，从而保证计算方法更具普适性。$(H+\lambda I)x=g$，当入较小时，$H$ 占主导，近似于高斯牛顿法，较大时，$\lambda * I$ 占主导，接近最速下降法。

4、Ceres 非线性最小二乘库

Ceres是一个用于求解非线性最小二乘问题的开源库，它可以用于许多优化和拟合问题。相关文档写的较为全面完善、原理也较为直观：http://ceres-solver.org/nnls_tutorial.html#numeric-derivatives。

Ceres 是一个用于求解各种非线性优化问题的开源 C++ 库, 它的设计理念是提供一个通用、高效、灵活和易于扩展的优化库，各种非线性优化问题能够被快速构建并求解。Ceres 求解的一般形式的最小二乘问题如下： $$ min {x} \frac{1}{2} \sum{i} \rho{i}\left(\left|f{i}\left(x{i{1}}, \cdots, x{i{n}}\right)\right|^{2}\right) \quad \text { s.t. } \quad l{i} \leq x{j} \leq u{j} $$ 该问题是一个带边界的核函数最小二乘问题，其中，$x_{1}, \cdots, x_{n}$ 在 Ceres 中被称为参数块 (Parameter Blocks)，表示优化变量，$\rho_{i}\left(\left|f_{i}\left(x_{i_{1}}, \cdots, x_{i_{n}}\right)\right|^{2}\right)$ 称为残差块 (Residual Blocks)，$f_{i}$ 称为代价函数 (Cost Function)，表示误差项或约束项。 $l_{i}$ 和 $u_{j}$ 分别表示 $x_{j}$ 的上下限，当 $l_{i}=-\infty, u_{j}=\infty$ 时，表示不限制 $x_{j}$ 的边界。目标函数由多个核函数 $\rho(\cdot)$ 求和构成，核函数的自变量为误差项的平方。 $\rho_{i}$ 也称为损失函数，主要用来消除异常点对求解过程的影响，通过抑制噪声的影响来获得较高的优化精度。若取 $\rho$ 为恒等函数，如 $\rho(s)=s$，则目标函数由多个误差项的平方和组成，得到无约束的最小二乘问题。

基本使用流程如下：

定义代价函数：首先，需要定义一个或多个代价函数，用于计算残差或误差的值。在此过程中，可以定义求导方式，包括自动求导（Auto Diff）、数值求导（Numeric Diff）和用户自定义的解析求导形式。
定义参数块：参数块表示需要优化的变量。Ceres 支持多种类型的参数块，包括一维数组、动态数组、特殊结构体和用户自定义类型等类型。在 SLAM 中，参数块通常被定义为四元数、李代数。添加参数块之前需要对定义好的参数块进行初始化，设定初始值。
定义问题对象：定义的问题对象可以用于管理代价函数和参数块。ceres 作用域下的 Problem 类包含多个成员函数，包括添加参数块函数、添加残差块函数、将某参数块设置为常量函数和设定参数块上下限函数等。
添加代价函数：使用 Problem 类中的成员函数将一个或多个代价函数添加到问题对象中。每个代价函数对应一个或多个参数块。
求解问题：求解问题通过调用 Solve 函数来实现。该函数的参数列表包括配置信息、问题对象指针和存储求解中各变量的信息的结构体的指针。配置信息定义在 Solver作用域下的 Options 结构体中，它的参数种类繁多，包括迭代求解方法、信赖域策略、求解器类型、最大迭代次数和最大求解时间等参数。通过 Ceres Solver 求解器求解非线性优化问题，最终输出优化后的变量。

Ceres 与 g2o 都是用于求解非线性优化问题的开源 C++库，但它们在设计理念和功能实现上有一些不同。g2o 的重点在于图优化，它专门用于解决图模型中的非线性优化问题。而 Ceres 则更注重于通用性，它可以用于解决各种类型的非线性最小二乘问题。

可以通过下面《视觉SLAM十四讲》中曲线拟合的示例来简单感受一下 Ceres 的使用：

#include <iostream>
#include <opencv2/core/core.hpp>
#include <ceres/ceres.h>
#include <chrono>

using namespace std;

// 代价函数的计算模型
struct CURVE_FITTING_COST {
  CURVE_FITTING_COST(double x, double y) : _x(x), _y(y) {}	// 成员列表初始化实现全残构造函数

  // 残差的计算，模板仿函数
  template<typename T>
  bool operator()(
    const T *const abc, // 模型参数，有3维
    T *residual) const {
	// 一维残差计算	
    residual[0] = T(_y) - ceres::exp(abc[0] * T(_x) * T(_x) + abc[1] * T(_x) + abc[2]); // y-exp(ax^2+bx+c)
    return true;
  }

  const double _x, _y;    // x,y数据
};

int main(int argc, char **argv) {
  double ar = 1.0, br = 2.0, cr = 1.0;         // 真实参数值
  double ae = 2.0, be = -1.0, ce = 5.0;        // 估计参数值
  int N = 100;                                 // 数据点
  double w_sigma = 1.0;                        // 噪声Sigma值
  double inv_sigma = 1.0 / w_sigma;
  cv::RNG rng;                                 // OpenCV随机数产生器

  vector<double> x_data, y_data;      // 数据
  for (int i = 0; i < N; i++) {
    double x = i / 100.0;
    x_data.push_back(x);
    y_data.push_back(exp(ar * x * x + br * x + cr) + rng.gaussian(w_sigma * w_sigma));
  }

  double abc[3] = {ae, be, ce};	// 定义估计变量 abc[3]，传入初值 ae、be、ce

  // 构建最小二乘问题
  ceres::Problem problem;	// 实例化 Problemn
  for (int i = 0; i < N; i++) {
    problem.AddResidualBlock(     // 向问题中添加残差项
      // 使用自动求导，模板参数：误差类型，输出维度，输入维度，维数要与前面struct中一致
      new ceres::AutoDiffCostFunction<CURVE_FITTING_COST, 1, 3>(
        new CURVE_FITTING_COST(x_data[i], y_data[i])
      ),
      nullptr,            // 核函数，这里不使用，为空。可以加核函数实现抗差
      abc                 // 待估计参数，计算出的增量往 abc 里面加
    );
  }

  // 配置求解器
  ceres::Solver::Options options;     // 这里有很多配置项可以填
  options.linear_solver_type = ceres::DENSE_NORMAL_CHOLESKY;  // 增量方程如何求解
  options.minimizer_progress_to_stdout = true;   // 输出到cout

  ceres::Solver::Summary summary;                // 优化信息
  chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
  ceres::Solve(options, &problem, &summary);  // 开始优化
  chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
  chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
  cout << "solve time cost = " << time_used.count() << " seconds. " << endl;

  // 输出结果
  cout << summary.BriefReport() << endl;
  cout << "estimated a,b,c = ";
  for (auto a:abc) cout << a << " ";
  cout << endl;

  return 0;
}

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

OB-GINS源码阅读.md

OB-GINS源码阅读.md

一、OB-GINS 简介

1、程序概述

2、相关论文

3、代码分析

4、第三方库

5、重点函数

6、执行流程

二、编译、调试

三、类型定义

四、主函数

1、函数调用关系图

2、执行流程图

3、读取配置文件

4、解算初始化

5、循环解算

6、解算结束

五、IMU 预积分

六、因子图优化

1、因子图模型

2、因子图优化状态估计模型

3、因子图优化求解

4、Ceres 非线性最小二乘库

Files

OB-GINS源码阅读.md

Latest commit

History

OB-GINS源码阅读.md

File metadata and controls

一、OB-GINS 简介

1、程序概述

2、相关论文

3、代码分析

4、第三方库

5、重点函数

6、执行流程

二、编译、调试

三、类型定义

四、主函数

1、函数调用关系图

2、执行流程图

3、读取配置文件

4、解算初始化

5、循环解算

6、解算结束

五、IMU 预积分

六、因子图优化

1、因子图模型

2、因子图优化状态估计模型

3、因子图优化求解

4、Ceres 非线性最小二乘库