diff --git a/README.fr-FR.md b/README.fr-FR.md
index c522c591e3..86a0fad385 100644
--- a/README.fr-FR.md
+++ b/README.fr-FR.md
@@ -3,11 +3,11 @@
[](https://travis-ci.org/trekhleb/javascript-algorithms)
[](https://codecov.io/gh/trekhleb/javascript-algorithms)
-Ce dépôt contient des exemples d'implémentation en JavaScript de plusieurs
+Ce dépôt contient des exemples d'implémentation en JavaScript de plusieurs
algorithmes et structures de données populaires.
-Chaque algorithme et structure de donnée possède son propre README contenant
-les explications détaillées et liens (incluant aussi des vidéos Youtube) pour
+Chaque algorithme et structure de donnée possède son propre README contenant
+les explications détaillées et liens (incluant aussi des vidéos Youtube) pour
complément d'informations.
_Lisez ceci dans d'autres langues:_
@@ -22,174 +22,178 @@ _Lisez ceci dans d'autres langues:_
## Data Structures
-Une structure de données est une manière spéciale d'organiser et de stocker
-des données dans un ordinateur de manière à ce que l'on puisse accéder à
-cette information et la modifier de manière efficiente. De manière plus
-spécifique, une structure de données est un ensemble composé d'une collection
-de valeurs, des relations entre ces valeurs ainsi que d'un ensemble de
+Une structure de données est une manière spéciale d'organiser et de stocker
+des données dans un ordinateur de manière à ce que l'on puisse accéder à
+cette information et la modifier de manière efficiente. De manière plus
+spécifique, une structure de données est un ensemble composé d'une collection
+de valeurs, des relations entre ces valeurs ainsi que d'un ensemble de
fonctions ou d'opérations pouvant être appliquées sur ces données.
`B` - Débutant, `A` - Avancé
-* `B` [Liste Chaînée](src/data-structures/linked-list)
-* `B` [Liste Doublement Chaînée](src/data-structures/doubly-linked-list)
-* `B` [Queue](src/data-structures/queue)
-* `B` [Pile](src/data-structures/stack)
-* `B` [Table de Hachage](src/data-structures/hash-table)
-* `B` [Tas](src/data-structures/heap)
-* `B` [Queue de Priorité](src/data-structures/priority-queue)
-* `A` [Trie](src/data-structures/trie)
-* `A` [Arbre](src/data-structures/tree)
- * `A` [Arbre de recherche Binaire](src/data-structures/tree/binary-search-tree)
- * `A` [Arbre AVL](src/data-structures/tree/avl-tree)
- * `A` [Arbre Red-Black](src/data-structures/tree/red-black-tree)
- * `A` [Arbre de Segments](src/data-structures/tree/segment-tree) - avec exemples de requêtes de type min/max/somme sur intervalles
- * `A` [Arbre de Fenwick](src/data-structures/tree/fenwick-tree) (Arbre Binaire Indexé)
-* `A` [Graphe](src/data-structures/graph) (orienté et non orienté)
-* `A` [Ensembles Disjoints](src/data-structures/disjoint-set)
-* `A` [Filtre de Bloom](src/data-structures/bloom-filter)
+- `B` [Liste Chaînée](src/data-structures/linked-list)
+- `B` [Liste Doublement Chaînée](src/data-structures/doubly-linked-list)
+- `B` [Queue](src/data-structures/queue)
+- `B` [Pile](src/data-structures/stack)
+- `B` [Table de Hachage](src/data-structures/hash-table)
+- `B` [Tas](src/data-structures/heap)
+- `B` [Queue de Priorité](src/data-structures/priority-queue)
+- `A` [Trie](src/data-structures/trie)
+- `A` [Arbre](src/data-structures/tree)
+ - `A` [Arbre de recherche Binaire](src/data-structures/tree/binary-search-tree)
+ - `A` [Arbre AVL](src/data-structures/tree/avl-tree)
+ - `A` [Arbre Red-Black](src/data-structures/tree/red-black-tree)
+ - `A` [Arbre de Segments](src/data-structures/tree/segment-tree) - avec exemples de requêtes de type min/max/somme sur intervalles
+ - `A` [Arbre de Fenwick](src/data-structures/tree/fenwick-tree) (Arbre Binaire Indexé)
+- `A` [Graphe](src/data-structures/graph) (orienté et non orienté)
+- `A` [Ensembles Disjoints](src/data-structures/disjoint-set)
+- `A` [Filtre de Bloom](src/data-structures/bloom-filter)
## Algorithmes
-Un algorithme est une démarche non ambigüe expliquant comment résoudre une
-classe de problèmes. C'est un ensemble de règles décrivant de manière précise
+Un algorithme est une démarche non ambigüe expliquant comment résoudre une
+classe de problèmes. C'est un ensemble de règles décrivant de manière précise
une séquence d'opérations.
`B` - Débutant, `A` - Avancé
### Algorithmes par topic
-* **Math**
- * `B` [Manipulation de Bit](src/algorithms/math/bits) - définir/obtenir/mettre à jour/effacer les bits, multiplication/division par deux, négativiser etc.
- * `B` [Factorielle](src/algorithms/math/factorial)
- * `B` [Nombre de Fibonacci](src/algorithms/math/fibonacci)
- * `B` [Test de Primalité](src/algorithms/math/primality-test) (méthode du test de division)
- * `B` [Algorithme d'Euclide](src/algorithms/math/euclidean-algorithm) - calcule le Plus Grand Commun Diviseur (PGCD)
- * `B` [Plus Petit Commun Multiple](src/algorithms/math/least-common-multiple) (PPCM)
- * `B` [Crible d'Eratosthène](src/algorithms/math/sieve-of-eratosthenes) - trouve tous les nombres premiers inférieurs à une certaine limite
- * `B` [Puissance de Deux](src/algorithms/math/is-power-of-two) - teste si un nombre donné est une puissance de deux (algorithmes naif et basé sur les opérations bit-à-bit)
- * `B` [Triangle de Pascal](src/algorithms/math/pascal-triangle)
- * `A` [Partition Entière](src/algorithms/math/integer-partition)
- * `A` [Approximation de π par l'algorithme de Liu Hui](src/algorithms/math/liu-hui) - approximation du calcul de π basé sur les N-gons
-* **Ensembles**
- * `B` [Produit Cartésien](src/algorithms/sets/cartesian-product) - produit de plusieurs ensembles
- * `B` [Mélange de Fisher–Yates](src/algorithms/sets/fisher-yates) - permulation aléatoire d'une séquence finie
- * `A` [Ensemble des parties d'un ensemble](src/algorithms/sets/power-set) - tous les sous-ensembles d'un ensemble
- * `A` [Permutations](src/algorithms/sets/permutations) (avec et sans répétitions)
- * `A` [Combinaisons](src/algorithms/sets/combinations) (avec et sans répétitions)
- * `A` [Plus Longue Sous-séquence Commune](src/algorithms/sets/longest-common-subsequence)
- * `A` [Plus Longue Sous-suite strictement croissante](src/algorithms/sets/longest-increasing-subsequence)
- * `A` [Plus Courte Super-séquence Commune](src/algorithms/sets/shortest-common-supersequence)
- * `A` [Problème du Sac à Dos](src/algorithms/sets/knapsack-problem) - versions "0/1" et "Sans Contraintes"
- * `A` [Sous-partie Maximum](src/algorithms/sets/maximum-subarray) - versions "Force Brute" et "Programmation Dynamique" (Kadane)
- * `A` [Somme combinatoire](src/algorithms/sets/combination-sum) - trouve toutes les combinaisons qui forment une somme spécifique
-* **Chaînes de Caractères**
- * `B` [Distance de Hamming](src/algorithms/string/hamming-distance) - nombre de positions auxquelles les symboles sont différents
- * `A` [Distance de Levenshtein](src/algorithms/string/levenshtein-distance) - distance minimale d'édition entre deux séquences
- * `A` [Algorithme de Knuth–Morris–Pratt](src/algorithms/string/knuth-morris-pratt) (Algorithme KMP) - recherche de sous-chaîne (pattern matching)
- * `A` [Algorithme Z](src/algorithms/string/z-algorithm) - recherche de sous-chaîne (pattern matching)
- * `A` [Algorithme de Rabin Karp](src/algorithms/string/rabin-karp) - recherche de sous-chaîne
- * `A` [Plus Longue Sous-chaîne Commune](src/algorithms/string/longest-common-substring)
- * `A` [Expression Régulière](src/algorithms/string/regular-expression-matching)
-* **Recherche**
- * `B` [Recherche Linéaire](src/algorithms/search/linear-search)
- * `B` [Jump Search](src/algorithms/search/jump-search) Recherche par saut (ou par bloc) - recherche dans une liste triée
- * `B` [Recherche Binaire](src/algorithms/search/binary-search) - recherche dans une liste triée
- * `B` [Recherche par Interpolation](src/algorithms/search/interpolation-search) - recherche dans une liste triée et uniformément distribuée
-* **Tri**
- * `B` [Tri Bullet](src/algorithms/sorting/bubble-sort)
- * `B` [Tri Sélection](src/algorithms/sorting/selection-sort)
- * `B` [Tri Insertion](src/algorithms/sorting/insertion-sort)
- * `B` [Tri Par Tas](src/algorithms/sorting/heap-sort)
- * `B` [Tri Fusion](src/algorithms/sorting/merge-sort)
- * `B` [Tri Rapide](src/algorithms/sorting/quick-sort) - implémentations *in-place* et *non in-place*
- * `B` [Tri Shell](src/algorithms/sorting/shell-sort)
- * `B` [Tri Comptage](src/algorithms/sorting/counting-sort)
- * `B` [Tri Radix](src/algorithms/sorting/radix-sort)
-* **Arbres**
- * `B` [Parcours en Profondeur](src/algorithms/tree/depth-first-search) (DFS)
- * `B` [Parcours en Largeur](src/algorithms/tree/breadth-first-search) (BFS)
-* **Graphes**
- * `B` [Parcours en Profondeur](src/algorithms/graph/depth-first-search) (DFS)
- * `B` [Parcours en Largeur](src/algorithms/graph/breadth-first-search) (BFS)
- * `B` [Algorithme de Kruskal](src/algorithms/graph/kruskal) - trouver l'arbre couvrant de poids minimal sur un graphe pondéré non dirigé
- * `A` [Algorithme de Dijkstra](src/algorithms/graph/dijkstra) - trouver tous les plus courts chemins partant d'un noeud vers tous les autres noeuds dans un graphe
- * `A` [Algorithme de Bellman-Ford](src/algorithms/graph/bellman-ford) - trouver tous les plus courts chemins partant d'un noeud vers tous les autres noeuds dans un graphe
- * `A` [Algorithme de Floyd-Warshall](src/algorithms/graph/floyd-warshall) - trouver tous les plus courts chemins entre toutes les paires de noeuds dans un graphe
- * `A` [Détection de Cycle](src/algorithms/graph/detect-cycle) - pour les graphes dirigés et non dirigés (implémentations basées sur l'algorithme de Parcours en Profondeur et sur les Ensembles Disjoints)
- * `A` [Algorithme de Prim](src/algorithms/graph/prim) - trouver l'arbre couvrant de poids minimal sur un graphe pondéré non dirigé
- * `A` [Tri Topologique](src/algorithms/graph/topological-sorting) - méthode DFS
- * `A` [Point d'Articulation](src/algorithms/graph/articulation-points) - algorithme de Tarjan (basé sur l'algorithme de Parcours en Profondeur)
- * `A` [Bridges](src/algorithms/graph/bridges) - algorithme basé sur le Parcours en Profondeur
- * `A` [Chemin Eulérien et Circuit Eulérien](src/algorithms/graph/eulerian-path) - algorithme de Fleury - visite chaque arc exactement une fois
- * `A` [Cycle Hamiltonien](src/algorithms/graph/hamiltonian-cycle) - visite chaque noeud exactement une fois
- * `A` [Composants Fortements Connexes](src/algorithms/graph/strongly-connected-components) - algorithme de Kosaraju
- * `A` [Problème du Voyageur de Commerce](src/algorithms/graph/travelling-salesman) - chemin le plus court visitant chaque cité et retournant à la cité d'origine
-* **Non catégorisé**
- * `B` [Tours de Hanoi](src/algorithms/uncategorized/hanoi-tower)
- * `B` [Rotation de Matrice Carrée](src/algorithms/uncategorized/square-matrix-rotation) - algorithme *in place*
- * `B` [Jump Game](src/algorithms/uncategorized/jump-game) - retour sur trace, programmation dynamique (haut-bas + bas-haut) et exemples gourmands
- * `B` [Chemins Uniques](src/algorithms/uncategorized/unique-paths) - retour sur trace, programmation dynamique (haut-bas + bas-haut) et exemples basés sur le Triangle de Pascal
- * `A` [Problème des N-Dames](src/algorithms/uncategorized/n-queens)
- * `A` [Problème du Cavalier](src/algorithms/uncategorized/knight-tour)
+- **Math**
+ - `B` [Manipulation de Bit](src/algorithms/math/bits/README.fr-FR.md) - définir/obtenir/mettre à jour/effacer les bits, multiplication/division par deux, négativiser etc.
+ - `B` [Factorielle](src/algorithms/math/factorial/README.fr-FR.md)
+ - `B` [Nombre de Fibonacci](src/algorithms/math/fibonacci/README.fr-FR.md)
+ - `B` [Test de Primalité](src/algorithms/math/primality-test) (méthode du test de division)
+ - `B` [Algorithme d'Euclide](src/algorithms/math/euclidean-algorithm/README.fr-FR.md) - calcule le Plus Grand Commun Diviseur (PGCD)
+ - `B` [Plus Petit Commun Multiple](src/algorithms/math/least-common-multiple) (PPCM)
+ - `B` [Crible d'Eratosthène](src/algorithms/math/sieve-of-eratosthenes) - trouve tous les nombres premiers inférieurs à une certaine limite
+ - `B` [Puissance de Deux](src/algorithms/math/is-power-of-two) - teste si un nombre donné est une puissance de deux (algorithmes naif et basé sur les opérations bit-à-bit)
+ - `B` [Triangle de Pascal](src/algorithms/math/pascal-triangle)
+ - `B` [Nombre complexe](src/algorithms/math/complex-number/README.fr-FR.md) - nombres complexes et opérations de bases
+ - `A` [Partition Entière](src/algorithms/math/integer-partition)
+ - `A` [Approximation de π par l'algorithme de Liu Hui](src/algorithms/math/liu-hui) - approximation du calcul de π basé sur les N-gons
+ - `B` [Exponentiation rapide](src/algorithms/math/fast-powering/README.fr-FR.md)
+ - `A` [Transformée de Fourier Discrète](src/algorithms/math/fourier-transform/README.fr-FR.md) - décomposer une fonction du temps (un signal) en fréquences qui la composent
+- **Ensembles**
+ - `B` [Produit Cartésien](src/algorithms/sets/cartesian-product) - produit de plusieurs ensembles
+ - `B` [Mélange de Fisher–Yates](src/algorithms/sets/fisher-yates) - permulation aléatoire d'une séquence finie
+ - `A` [Ensemble des parties d'un ensemble](src/algorithms/sets/power-set) - tous les sous-ensembles d'un ensemble
+ - `A` [Permutations](src/algorithms/sets/permutations) (avec et sans répétitions)
+ - `A` [Combinaisons](src/algorithms/sets/combinations) (avec et sans répétitions)
+ - `A` [Plus Longue Sous-séquence Commune](src/algorithms/sets/longest-common-subsequence)
+ - `A` [Plus Longue Sous-suite strictement croissante](src/algorithms/sets/longest-increasing-subsequence)
+ - `A` [Plus Courte Super-séquence Commune](src/algorithms/sets/shortest-common-supersequence)
+ - `A` [Problème du Sac à Dos](src/algorithms/sets/knapsack-problem) - versions "0/1" et "Sans Contraintes"
+ - `A` [Sous-partie Maximum](src/algorithms/sets/maximum-subarray) - versions "Force Brute" et "Programmation Dynamique" (Kadane)
+ - `A` [Somme combinatoire](src/algorithms/sets/combination-sum) - trouve toutes les combinaisons qui forment une somme spécifique
+- **Chaînes de Caractères**
+ - `B` [Distance de Hamming](src/algorithms/string/hamming-distance) - nombre de positions auxquelles les symboles sont différents
+ - `A` [Distance de Levenshtein](src/algorithms/string/levenshtein-distance) - distance minimale d'édition entre deux séquences
+ - `A` [Algorithme de Knuth–Morris–Pratt](src/algorithms/string/knuth-morris-pratt) (Algorithme KMP) - recherche de sous-chaîne (pattern matching)
+ - `A` [Algorithme Z](src/algorithms/string/z-algorithm) - recherche de sous-chaîne (pattern matching)
+ - `A` [Algorithme de Rabin Karp](src/algorithms/string/rabin-karp) - recherche de sous-chaîne
+ - `A` [Plus Longue Sous-chaîne Commune](src/algorithms/string/longest-common-substring)
+ - `A` [Expression Régulière](src/algorithms/string/regular-expression-matching)
+- **Recherche**
+ - `B` [Recherche Linéaire](src/algorithms/search/linear-search)
+ - `B` [Jump Search](src/algorithms/search/jump-search) Recherche par saut (ou par bloc) - recherche dans une liste triée
+ - `B` [Recherche Binaire](src/algorithms/search/binary-search) - recherche dans une liste triée
+ - `B` [Recherche par Interpolation](src/algorithms/search/interpolation-search) - recherche dans une liste triée et uniformément distribuée
+- **Tri**
+ - `B` [Tri Bullet](src/algorithms/sorting/bubble-sort)
+ - `B` [Tri Sélection](src/algorithms/sorting/selection-sort)
+ - `B` [Tri Insertion](src/algorithms/sorting/insertion-sort)
+ - `B` [Tri Par Tas](src/algorithms/sorting/heap-sort)
+ - `B` [Tri Fusion](src/algorithms/sorting/merge-sort)
+ - `B` [Tri Rapide](src/algorithms/sorting/quick-sort) - implémentations _in-place_ et _non in-place_
+ - `B` [Tri Shell](src/algorithms/sorting/shell-sort)
+ - `B` [Tri Comptage](src/algorithms/sorting/counting-sort)
+ - `B` [Tri Radix](src/algorithms/sorting/radix-sort)
+- **Arbres**
+ - `B` [Parcours en Profondeur](src/algorithms/tree/depth-first-search) (DFS)
+ - `B` [Parcours en Largeur](src/algorithms/tree/breadth-first-search) (BFS)
+- **Graphes**
+ - `B` [Parcours en Profondeur](src/algorithms/graph/depth-first-search) (DFS)
+ - `B` [Parcours en Largeur](src/algorithms/graph/breadth-first-search) (BFS)
+ - `B` [Algorithme de Kruskal](src/algorithms/graph/kruskal) - trouver l'arbre couvrant de poids minimal sur un graphe pondéré non dirigé
+ - `A` [Algorithme de Dijkstra](src/algorithms/graph/dijkstra) - trouver tous les plus courts chemins partant d'un noeud vers tous les autres noeuds dans un graphe
+ - `A` [Algorithme de Bellman-Ford](src/algorithms/graph/bellman-ford) - trouver tous les plus courts chemins partant d'un noeud vers tous les autres noeuds dans un graphe
+ - `A` [Algorithme de Floyd-Warshall](src/algorithms/graph/floyd-warshall) - trouver tous les plus courts chemins entre toutes les paires de noeuds dans un graphe
+ - `A` [Détection de Cycle](src/algorithms/graph/detect-cycle) - pour les graphes dirigés et non dirigés (implémentations basées sur l'algorithme de Parcours en Profondeur et sur les Ensembles Disjoints)
+ - `A` [Algorithme de Prim](src/algorithms/graph/prim) - trouver l'arbre couvrant de poids minimal sur un graphe pondéré non dirigé
+ - `A` [Tri Topologique](src/algorithms/graph/topological-sorting) - méthode DFS
+ - `A` [Point d'Articulation](src/algorithms/graph/articulation-points) - algorithme de Tarjan (basé sur l'algorithme de Parcours en Profondeur)
+ - `A` [Bridges](src/algorithms/graph/bridges) - algorithme basé sur le Parcours en Profondeur
+ - `A` [Chemin Eulérien et Circuit Eulérien](src/algorithms/graph/eulerian-path) - algorithme de Fleury - visite chaque arc exactement une fois
+ - `A` [Cycle Hamiltonien](src/algorithms/graph/hamiltonian-cycle) - visite chaque noeud exactement une fois
+ - `A` [Composants Fortements Connexes](src/algorithms/graph/strongly-connected-components) - algorithme de Kosaraju
+ - `A` [Problème du Voyageur de Commerce](src/algorithms/graph/travelling-salesman) - chemin le plus court visitant chaque cité et retournant à la cité d'origine
+- **Non catégorisé**
+ - `B` [Tours de Hanoi](src/algorithms/uncategorized/hanoi-tower)
+ - `B` [Rotation de Matrice Carrée](src/algorithms/uncategorized/square-matrix-rotation) - algorithme _in place_
+ - `B` [Jump Game](src/algorithms/uncategorized/jump-game) - retour sur trace, programmation dynamique (haut-bas + bas-haut) et exemples gourmands
+ - `B` [Chemins Uniques](src/algorithms/uncategorized/unique-paths) - retour sur trace, programmation dynamique (haut-bas + bas-haut) et exemples basés sur le Triangle de Pascal
+ - `A` [Problème des N-Dames](src/algorithms/uncategorized/n-queens)
+ - `A` [Problème du Cavalier](src/algorithms/uncategorized/knight-tour)
### Algorithmes par Paradigme
-Un paradigme algorithmique est une méthode générique ou une approche qui
-sous-tend la conception d'une classe d'algorithmes. C'est une abstraction
-au-dessus de la notion d'algorithme, tout comme l'algorithme est une abstraction
+Un paradigme algorithmique est une méthode générique ou une approche qui
+sous-tend la conception d'une classe d'algorithmes. C'est une abstraction
+au-dessus de la notion d'algorithme, tout comme l'algorithme est une abstraction
supérieure à un programme informatique.
-* **Force Brute** - cherche parmi toutes les possibilités et retient la meilleure
- * `B` [Recherche Linéaire](src/algorithms/search/linear-search)
- * `A` [Sous-partie Maximum](src/algorithms/sets/maximum-subarray)
- * `A` [Problème du Voyageur de Commerce](src/algorithms/graph/travelling-salesman) - chemin le plus court visitant chaque cité et retournant à la cité d'origine
-* **Gourmand** - choisit la meilleure option à l'instant courant, sans tenir compte de la situation future
- * `B` [Jump Game](src/algorithms/uncategorized/jump-game)
- * `A` [Problème du Sac à Dos Sans Contraintes](src/algorithms/sets/knapsack-problem)
- * `A` [Algorithme de Dijkstra](src/algorithms/graph/dijkstra) - trouver tous les plus courts chemins partant d'un noeud vers tous les autres noeuds dans un graphe
- * `A` [Algorithme de Prim](src/algorithms/graph/prim) - trouver l'arbre couvrant de poids minimal sur un graphe pondéré non dirigé
- * `A` [Algorithme de Kruskal](src/algorithms/graph/kruskal) - trouver l'arbre couvrant de poids minimal sur un graphe pondéré non dirigé
-* **Diviser et Régner** - divise le problème en sous problèmes (plus simples) et résoud ces sous problèmes
- * `B` [Recherche Binaire](src/algorithms/search/binary-search)
- * `B` [Tours de Hanoi](src/algorithms/uncategorized/hanoi-tower)
- * `B` [Triangle de Pascal](src/algorithms/math/pascal-triangle)
- * `B` [Algorithme d'Euclide](src/algorithms/math/euclidean-algorithm) - calcule le Plus Grand Commun Diviseur (PGCD)
- * `B` [Tri Fusion](src/algorithms/sorting/merge-sort)
- * `B` [Tri Rapide](src/algorithms/sorting/quick-sort)
- * `B` [Arbre de Parcours en Profondeur](src/algorithms/tree/depth-first-search) (DFS)
- * `B` [Graphe de Parcours en Profondeur](src/algorithms/graph/depth-first-search) (DFS)
- * `B` [Jump Game](src/algorithms/uncategorized/jump-game)
- * `A` [Permutations](src/algorithms/sets/permutations) (avec et sans répétitions)
- * `A` [Combinations](src/algorithms/sets/combinations) (avec et sans répétitions)
-* **Programmation Dynamique** - construit une solution en utilisant les solutions précédemment trouvées
- * `B` [Nombre de Fibonacci](src/algorithms/math/fibonacci)
- * `B` [Jump Game](src/algorithms/uncategorized/jump-game)
- * `B` [Chemins Uniques](src/algorithms/uncategorized/unique-paths)
- * `A` [Distance de Levenshtein](src/algorithms/string/levenshtein-distance) - distance minimale d'édition entre deux séquences
- * `A` [Plus Longue Sous-séquence Commune](src/algorithms/sets/longest-common-subsequence)
- * `A` [Plus Longue Sous-chaîne Commune](src/algorithms/string/longest-common-substring)
- * `A` [Plus Longue Sous-suite strictement croissante](src/algorithms/sets/longest-increasing-subsequence)
- * `A` [Plus Courte Super-séquence Commune](src/algorithms/sets/shortest-common-supersequence)
- * `A` [Problème de Sac à Dos](src/algorithms/sets/knapsack-problem)
- * `A` [Partition Entière](src/algorithms/math/integer-partition)
- * `A` [Sous-partie Maximum](src/algorithms/sets/maximum-subarray)
- * `A` [Algorithme de Bellman-Ford](src/algorithms/graph/bellman-ford) - trouver tous les plus courts chemins partant d'un noeud vers tous les autres noeuds dans un graphe
- * `A` [Algorithme de Floyd-Warshall](src/algorithms/graph/floyd-warshall) - trouver tous les plus courts chemins entre toutes les paires de noeuds dans un graphe
- * `A` [Expression Régulière](src/algorithms/string/regular-expression-matching)
-* **Retour sur trace** - de même que la version "Force Brute", essaie de générer toutes les solutions possibles, mais pour chaque solution générée, on teste si elle satisfait toutes les conditions, et seulement ensuite continuer à générer des solutions ultérieures. Sinon, l'on revient en arrière, et l'on essaie un
-chemin différent pour tester d'autres solutions. Normalement, la traversée en profondeur de l'espace d'états est utilisée.
- * `B` [Jump Game](src/algorithms/uncategorized/jump-game)
- * `B` [Unique Paths](src/algorithms/uncategorized/unique-paths)
- * `A` [Hamiltonian Cycle](src/algorithms/graph/hamiltonian-cycle) - Visit every vertex exactly once
- * `A` [Problème des N-Dames](src/algorithms/uncategorized/n-queens)
- * `A` [Problème du Cavalier](src/algorithms/uncategorized/knight-tour)
- * `A` [Somme combinatoire](src/algorithms/sets/combination-sum) - trouve toutes les combinaisons qui forment une somme spécifique
-* **Séparation et Evaluation** - pemet de retenir une solution à moindre coût dans un ensemble. Pour chaque étape, l'on garde une trace de la solution la moins coûteuse trouvée jusqu'à présent en tant que borne inférieure du coût. Cela afin d'éliminer les solutions partielles dont les coûts sont plus élevés que celui de la solution actuelle retenue. Normalement, la traversée en largeur en combinaison avec la traversée en profondeur de l'espace d'états de l'arbre est utilisée.
+- **Force Brute** - cherche parmi toutes les possibilités et retient la meilleure
+ - `B` [Recherche Linéaire](src/algorithms/search/linear-search)
+ - `A` [Sous-partie Maximum](src/algorithms/sets/maximum-subarray)
+ - `A` [Problème du Voyageur de Commerce](src/algorithms/graph/travelling-salesman) - chemin le plus court visitant chaque cité et retournant à la cité d'origine
+- **Gourmand** - choisit la meilleure option à l'instant courant, sans tenir compte de la situation future
+ - `B` [Jump Game](src/algorithms/uncategorized/jump-game)
+ - `A` [Problème du Sac à Dos Sans Contraintes](src/algorithms/sets/knapsack-problem)
+ - `A` [Algorithme de Dijkstra](src/algorithms/graph/dijkstra) - trouver tous les plus courts chemins partant d'un noeud vers tous les autres noeuds dans un graphe
+ - `A` [Algorithme de Prim](src/algorithms/graph/prim) - trouver l'arbre couvrant de poids minimal sur un graphe pondéré non dirigé
+ - `A` [Algorithme de Kruskal](src/algorithms/graph/kruskal) - trouver l'arbre couvrant de poids minimal sur un graphe pondéré non dirigé
+- **Diviser et Régner** - divise le problème en sous problèmes (plus simples) et résoud ces sous problèmes
+ - `B` [Recherche Binaire](src/algorithms/search/binary-search)
+ - `B` [Tours de Hanoi](src/algorithms/uncategorized/hanoi-tower)
+ - `B` [Triangle de Pascal](src/algorithms/math/pascal-triangle)
+ - `B` [Algorithme d'Euclide](src/algorithms/math/euclidean-algorithm) - calcule le Plus Grand Commun Diviseur (PGCD)
+ - `B` [Tri Fusion](src/algorithms/sorting/merge-sort)
+ - `B` [Tri Rapide](src/algorithms/sorting/quick-sort)
+ - `B` [Arbre de Parcours en Profondeur](src/algorithms/tree/depth-first-search) (DFS)
+ - `B` [Graphe de Parcours en Profondeur](src/algorithms/graph/depth-first-search) (DFS)
+ - `B` [Jump Game](src/algorithms/uncategorized/jump-game)
+ - `A` [Permutations](src/algorithms/sets/permutations) (avec et sans répétitions)
+ - `A` [Combinations](src/algorithms/sets/combinations) (avec et sans répétitions)
+- **Programmation Dynamique** - construit une solution en utilisant les solutions précédemment trouvées
+ - `B` [Nombre de Fibonacci](src/algorithms/math/fibonacci)
+ - `B` [Jump Game](src/algorithms/uncategorized/jump-game)
+ - `B` [Chemins Uniques](src/algorithms/uncategorized/unique-paths)
+ - `A` [Distance de Levenshtein](src/algorithms/string/levenshtein-distance) - distance minimale d'édition entre deux séquences
+ - `A` [Plus Longue Sous-séquence Commune](src/algorithms/sets/longest-common-subsequence)
+ - `A` [Plus Longue Sous-chaîne Commune](src/algorithms/string/longest-common-substring)
+ - `A` [Plus Longue Sous-suite strictement croissante](src/algorithms/sets/longest-increasing-subsequence)
+ - `A` [Plus Courte Super-séquence Commune](src/algorithms/sets/shortest-common-supersequence)
+ - `A` [Problème de Sac à Dos](src/algorithms/sets/knapsack-problem)
+ - `A` [Partition Entière](src/algorithms/math/integer-partition)
+ - `A` [Sous-partie Maximum](src/algorithms/sets/maximum-subarray)
+ - `A` [Algorithme de Bellman-Ford](src/algorithms/graph/bellman-ford) - trouver tous les plus courts chemins partant d'un noeud vers tous les autres noeuds dans un graphe
+ - `A` [Algorithme de Floyd-Warshall](src/algorithms/graph/floyd-warshall) - trouver tous les plus courts chemins entre toutes les paires de noeuds dans un graphe
+ - `A` [Expression Régulière](src/algorithms/string/regular-expression-matching)
+- **Retour sur trace** - de même que la version "Force Brute", essaie de générer toutes les solutions possibles, mais pour chaque solution générée, on teste si elle satisfait toutes les conditions, et seulement ensuite continuer à générer des solutions ultérieures. Sinon, l'on revient en arrière, et l'on essaie un
+ chemin différent pour tester d'autres solutions. Normalement, la traversée en profondeur de l'espace d'états est utilisée.
+ - `B` [Jump Game](src/algorithms/uncategorized/jump-game)
+ - `B` [Unique Paths](src/algorithms/uncategorized/unique-paths)
+ - `A` [Hamiltonian Cycle](src/algorithms/graph/hamiltonian-cycle) - Visit every vertex exactly once
+ - `A` [Problème des N-Dames](src/algorithms/uncategorized/n-queens)
+ - `A` [Problème du Cavalier](src/algorithms/uncategorized/knight-tour)
+ - `A` [Somme combinatoire](src/algorithms/sets/combination-sum) - trouve toutes les combinaisons qui forment une somme spécifique
+- **Séparation et Evaluation** - pemet de retenir une solution à moindre coût dans un ensemble. Pour chaque étape, l'on garde une trace de la solution la moins coûteuse trouvée jusqu'à présent en tant que borne inférieure du coût. Cela afin d'éliminer les solutions partielles dont les coûts sont plus élevés que celui de la solution actuelle retenue. Normalement, la traversée en largeur en combinaison avec la traversée en profondeur de l'espace d'états de l'arbre est utilisée.
## Comment utiliser ce dépôt
**Installer toutes les dépendances**
+
```
npm install
```
@@ -203,22 +207,24 @@ npm run lint
```
**Exécuter tous les tests**
+
```
npm test
```
**Exécuter les tests par nom**
+
```
npm test -- 'LinkedList'
```
**Tests personnalisés**
-Vous pouvez manipuler les structures de données et algorithmes présents dans ce
-dépôt avec le fichier `./src/playground/playground.js` et écrire vos propres
+Vous pouvez manipuler les structures de données et algorithmes présents dans ce
+dépôt avec le fichier `./src/playground/playground.js` et écrire vos propres
tests dans file `./src/playground/__test__/playground.test.js`.
-Vous pourrez alors simplement exécuter la commande suivante afin de tester si
+Vous pourrez alors simplement exécuter la commande suivante afin de tester si
votre code fonctionne comme escompté
```
@@ -239,44 +245,44 @@ Comparaison de la performance d'algorithmes en notation Grand O.
Source: [Big O Cheat Sheet](http://bigocheatsheet.com/).
-Voici la liste de certaines des notations Grand O les plus utilisées et de leurs
+Voici la liste de certaines des notations Grand O les plus utilisées et de leurs
comparaisons de performance suivant différentes tailles pour les données d'entrée.
-| Notation Grand O | Opérations pour 10 éléments | Opérations pour 100 éléments | Opérations pour 1000 éléments |
-| ---------------- | ---------------------------- | ----------------------------- | ------------------------------- |
-| **O(1)** | 1 | 1 | 1 |
-| **O(log N)** | 3 | 6 | 9 |
-| **O(N)** | 10 | 100 | 1000 |
-| **O(N log N)** | 30 | 600 | 9000 |
-| **O(N^2)** | 100 | 10000 | 1000000 |
-| **O(2^N)** | 1024 | 1.26e+29 | 1.07e+301 |
-| **O(N!)** | 3628800 | 9.3e+157 | 4.02e+2567 |
+| Notation Grand O | Opérations pour 10 éléments | Opérations pour 100 éléments | Opérations pour 1000 éléments |
+| ---------------- | --------------------------- | ---------------------------- | ----------------------------- |
+| **O(1)** | 1 | 1 | 1 |
+| **O(log N)** | 3 | 6 | 9 |
+| **O(N)** | 10 | 100 | 1000 |
+| **O(N log N)** | 30 | 600 | 9000 |
+| **O(N^2)** | 100 | 10000 | 1000000 |
+| **O(2^N)** | 1024 | 1.26e+29 | 1.07e+301 |
+| **O(N!)** | 3628800 | 9.3e+157 | 4.02e+2567 |
### Complexité des Opérations suivant les Structures de Données
-| Structure de donnée | Accès | Recherche | Insertion | Suppression | Commentaires |
-| ------------------------------- | :-------: | :-------: | :-------: | :----------: | :------------ |
-| **Liste** | 1 | n | n | n | |
-| **Pile** | n | n | 1 | 1 | |
-| **Queue** | n | n | 1 | 1 | |
-| **Liste Liée** | n | n | 1 | 1 | |
-| **Table de Hachage** | - | n | n | n | Dans le cas des fonctions de hachage parfaites, les couts seraient de O(1) |
-| **Arbre de Recherche Binaire** | n | n | n | n | Dans le cas des arbre équilibrés, les coûts seraient de O(log(n)) |
-| **Arbre B** | log(n) | log(n) | log(n) | log(n) | |
-| **Arbre Red-Black** | log(n) | log(n) | log(n) | log(n) | |
-| **Arbre AVL** | log(n) | log(n) | log(n) | log(n) | |
-| **Filtre de Bloom** | - | 1 | 1 | - | Les faux positifs sont possibles lors de la recherche |
+| Structure de donnée | Accès | Recherche | Insertion | Suppression | Commentaires |
+| ------------------------------ | :----: | :-------: | :-------: | :---------: | :------------------------------------------------------------------------- |
+| **Liste** | 1 | n | n | n | |
+| **Pile** | n | n | 1 | 1 | |
+| **Queue** | n | n | 1 | 1 | |
+| **Liste Liée** | n | n | 1 | 1 | |
+| **Table de Hachage** | - | n | n | n | Dans le cas des fonctions de hachage parfaites, les couts seraient de O(1) |
+| **Arbre de Recherche Binaire** | n | n | n | n | Dans le cas des arbre équilibrés, les coûts seraient de O(log(n)) |
+| **Arbre B** | log(n) | log(n) | log(n) | log(n) | |
+| **Arbre Red-Black** | log(n) | log(n) | log(n) | log(n) | |
+| **Arbre AVL** | log(n) | log(n) | log(n) | log(n) | |
+| **Filtre de Bloom** | - | 1 | 1 | - | Les faux positifs sont possibles lors de la recherche |
### Complexité des Algorithmes de Tri de Liste
-| Nom | Meilleur | Moyenne | Pire | Mémoire | Stable | Commentaires |
-| ----------------------- | :-------------: | :--------------------: | :-----------------: | :-------: | :-------: | :------------ |
-| **Tri Bulle** | n | n2 | n2 | 1 | Oui | |
-| **Tri Insertion** | n | n2 | n2 | 1 | Oui | |
-| **Tri Sélection** | n2 | n2 | n2 | 1 | Non | |
-| **Tri par Tas** | n log(n) | n log(n) | n log(n) | 1 | Non | |
-| **Merge sort** | n log(n) | n log(n) | n log(n) | n | Oui | |
-| **Tri Rapide** | n log(n) | n log(n) | n2 | log(n) | Non | le Tri Rapide est généralement effectué *in-place* avec une pile de taille O(log(n)) |
-| **Tri Shell** | n log(n) | dépend du gap séquence | n (log(n))2 | 1 | Non | |
-| **Tri Comptage** | n + r | n + r | n + r | n + r | Oui | r - le plus grand nombre dans la liste |
-| **Tri Radix** | n * k | n * k | n * k | n + k | Non | k - longueur du plus long index |
+| Nom | Meilleur | Moyenne | Pire | Mémoire | Stable | Commentaires |
+| ----------------- | :-----------: | :--------------------: | :-------------------------: | :-----: | :----: | :----------------------------------------------------------------------------------- |
+| **Tri Bulle** | n | n2 | n2 | 1 | Oui | |
+| **Tri Insertion** | n | n2 | n2 | 1 | Oui | |
+| **Tri Sélection** | n2 | n2 | n2 | 1 | Non | |
+| **Tri par Tas** | n log(n) | n log(n) | n log(n) | 1 | Non | |
+| **Merge sort** | n log(n) | n log(n) | n log(n) | n | Oui | |
+| **Tri Rapide** | n log(n) | n log(n) | n2 | log(n) | Non | le Tri Rapide est généralement effectué _in-place_ avec une pile de taille O(log(n)) |
+| **Tri Shell** | n log(n) | dépend du gap séquence | n (log(n))2 | 1 | Non | |
+| **Tri Comptage** | n + r | n + r | n + r | n + r | Oui | r - le plus grand nombre dans la liste |
+| **Tri Radix** | n \* k | n \* k | n \* k | n + k | Non | k - longueur du plus long index |
diff --git a/src/algorithms/math/bits/README.fr-FR.md b/src/algorithms/math/bits/README.fr-FR.md
new file mode 100644
index 0000000000..a831ae22ad
--- /dev/null
+++ b/src/algorithms/math/bits/README.fr-FR.md
@@ -0,0 +1,295 @@
+# Manipulation de bits
+
+_Read this in other languages:_
+[english](README.md).
+
+#### Vérifier un bit (_get_)
+
+Cette méthode décale le bit correspondant (_bit shifting_) à la position zéro.
+Ensuite, nous exécutons l'opération `AND` avec un masque comme `0001`.
+Cela efface tous les bits du nombre original sauf le correspondant.
+Si le bit pertinent est `1`, le résultat est `1`, sinon le résultat est `0`.
+
+> Voir [getBit.js](getBit.js) pour plus de détails.
+
+#### Mettre un bit à 1(_set_)
+
+Cette méthode met un bit à `1` en fonction d'un rang (`bitPosition`),
+créant ainsi une valeur qui ressemble à `00100`.
+Ensuite, nous effectuons l'opération `OU` qui met un bit spécifique
+en `1` sans affecter les autres bits du nombre.
+
+> Voir [setBit.js](setBit.js) pour plus de détails.
+
+#### Mettre un bit à 0 (_clear_)
+
+Cette méthode met un bit à `1` en fonction d'un rang (`bitPosition`),
+créant ainsi une valeur qui ressemble à `00100`.
+Puis on inverse ce masque de bits pour obtenir un nombre ressemblant à `11011`.
+Enfin, l'opération `AND` est appliquée au nombre et au masque.
+Cette opération annule le bit.
+
+> Voir [clearBit.js](clearBit.js) pour plus de détails.
+
+#### Mettre à jour un Bit (_update_)
+
+Cette méthode est une combinaison de l'"annulation de bit"
+et du "forçage de bit".
+
+> Voir [updateBit.js](updateBit.js) pour plus de détails.
+
+#### Vérifier si un nombre est pair (_isEven_)
+
+Cette méthode détermine si un nombre donné est pair.
+Elle s'appuie sur le fait que les nombres impairs ont leur dernier
+bit droit à `1`.
+
+```text
+Nombre: 5 = 0b0101
+isEven: false
+
+Nombre: 4 = 0b0100
+isEven: true
+```
+
+> Voir [isEven.js](isEven.js) pour plus de détails.
+
+#### Vérifier si un nombre est positif (_isPositive_)
+
+Cette méthode détermine un le nombre donné est positif.
+Elle s'appuie sur le fait que tous les nombres positifs
+ont leur bit le plus à gauche à `0`.
+Cependant, si le nombre fourni est zéro
+ou zéro négatif, il doit toujours renvoyer `false`.
+
+```text
+Nombre: 1 = 0b0001
+isPositive: true
+
+Nombre: -1 = -0b0001
+isPositive: false
+```
+
+> Voir [isPositive.js](isPositive.js) pour plus de détails.
+
+#### Multiplier par deux
+
+Cette méthode décale un nombre donné d'un bit vers la gauche.
+Ainsi, toutes les composantes du nombre binaire (en puissances de deux) sont
+multipliées par deux et donc le nombre lui-même est
+multiplié par deux.
+
+```
+Avant le décalage
+Nombre: 0b0101 = 5
+Puissances de deux: 0 + 2^2 + 0 + 2^0
+
+Après le décalage
+Nombre: 0b1010 = 10
+Puissances de deux: 2^3 + 0 + 2^1 + 0
+```
+
+> Voir [multiplyByTwo.js](multiplyByTwo.js) pour plus de détails.
+
+#### Diviser par deux
+
+Cette méthode décale un nombre donné d'un bit vers la droite.
+Ainsi, toutes les composantes du nombre binaire (en puissances de deux) sont
+divisées par deux et donc le nombre lui-même est
+divisé par deux, sans reste.
+
+```
+Avant le décalage
+Nombre: 0b0101 = 5
+Puissances de deux: 0 + 2^2 + 0 + 2^0
+
+Après le décalage
+Nombre: 0b0010 = 2
+Puissances de deux: 0 + 0 + 2^1 + 0
+```
+
+> Voir [divideByTwo.js](divideByTwo.js) pour plus de détails.
+
+#### Inverser le signe (_Switch Sign_)
+
+Cette méthode rend positifs les nombres négatifs, et vice-versa.
+Pour ce faire, elle s'appuie sur l'approche "Complément à deux",
+qui inverse tous les bits du nombre et y ajoute 1.
+
+```
+1101 -3
+1110 -2
+1111 -1
+0000 0
+0001 1
+0010 2
+0011 3
+```
+
+> Voir [switchSign.js](switchSign.js) pour plus de détails.
+
+#### Multiplier deux nombres signés
+
+Cette méthode multiplie deux nombres entiers signés
+à l'aide d'opérateurs bit à bit.
+Cette méthode est basée sur les faits suivants:
+
+```text
+a * b peut être écrit sous les formes suivantes:
+ 0 si a est zero ou b est zero ou les deux sont zero
+ 2a * (b/2) si b est pair
+ 2a * (b - 1)/2 + a si b est impair et positif
+ 2a * (b + 1)/2 - a si b est impair et negatif
+```
+
+L'avantage de cette approche est qu'à chaque étape de la récursion
+l'un des opérandes est réduit à la moitié de sa valeur d'origine.
+Par conséquent, la complexité d'exécution est `O(log(b))`
+où `b` est l'opérande qui se réduit de moitié à chaque récursion.
+
+> Voir [multiply.js](multiply.js) pour plus de détails.
+
+#### Multiplier deux nombres positifs
+
+Cette méthode multiplie deux nombres entiers à l'aide d'opérateurs bit à bit.
+Cette méthode s'appuie sur le fait que "Chaque nombre peut être lu
+comme une somme de puissances de 2".
+
+L'idée principale de la multiplication bit à bit
+est que chaque nombre peut être divisé en somme des puissances de deux:
+
+Ainsi
+
+```text
+19 = 2^4 + 2^1 + 2^0
+```
+
+Donc multiplier `x` par `19` est equivalent à :
+
+```text
+x * 19 = x * 2^4 + x * 2^1 + x * 2^0
+```
+
+Nous devons maintenant nous rappeler que `x * 2 ^ 4` équivaut
+à déplacer`x` vers la gauche par `4` bits (`x << 4`).
+
+> Voir [multiplyUnsigned.js](multiplyUnsigned.js) pour plus de détails.
+
+#### Compter les bits à 1
+
+This method counts the number of set bits in a number using bitwise operators.
+The main idea is that we shift the number right by one bit at a time and check
+the result of `&` operation that is `1` if bit is set and `0` otherwise.
+
+Cette méthode décompte les bits à `1` d'un nombre
+à l'aide d'opérateurs bit à bit.
+L'idée principale est de décaler le nombre vers la droite, un bit à la fois,
+et de vérifier le résultat de l'opération `&` :
+`1` si le bit est défini et `0` dans le cas contraire.
+
+```text
+Nombre: 5 = 0b0101
+Décompte des bits à 1 = 2
+```
+
+> Voir [countSetBits.js](countSetBits.js) pour plus de détails.
+
+#### Compter les bits nécessaire pour remplacer un nombre
+
+This methods outputs the number of bits required to convert one number to another.
+This makes use of property that when numbers are `XOR`-ed the result will be number
+of different bits.
+
+Cette méthode retourne le nombre de bits requis
+pour convertir un nombre en un autre.
+Elle repose sur la propriété suivante:
+lorsque les nombres sont évalués via `XOR`, le résultat est le nombre
+de bits différents entre les deux.
+
+```
+5 = 0b0101
+1 = 0b0001
+Nombre de bits pour le remplacement: 1
+```
+
+> Voir [bitsDiff.js](bitsDiff.js) pour plus de détails.
+
+#### Calculer les bits significatifs d'un nombre
+
+Pour connaître les bits significatifs d'un nombre,
+on peut décaler `1` d'un bit à gauche plusieurs fois d'affilée
+jusqu'à ce que ce nombre soit plus grand que le nombre à comparer.
+
+```
+5 = 0b0101
+Décompte des bits significatifs: 3
+On décale 1 quatre fois pour dépasser 5.
+```
+
+> Voir [bitLength.js](bitLength.js) pour plus de détails.
+
+#### Vérifier si un nombre est une puissance de 2
+
+Cette méthode vérifie si un nombre donné est une puissance de deux.
+Elle s'appuie sur la propriété suivante.
+Disons que `powerNumber` est une puissance de deux (c'est-à-dire 2, 4, 8, 16 etc.).
+Si nous faisons l'opération `&` entre `powerNumber` et `powerNumber - 1`,
+elle retournera`0` (dans le cas où le nombre est une puissance de deux).
+
+```
+Nombre: 4 = 0b0100
+Nombre: 3 = (4 - 1) = 0b0011
+4 & 3 = 0b0100 & 0b0011 = 0b0000 <-- Égal à zéro, car c'est une puissance de 2.
+
+Nombre: 10 = 0b01010
+Nombre: 9 = (10 - 1) = 0b01001
+10 & 9 = 0b01010 & 0b01001 = 0b01000 <-- Différent de 0, donc n'est pas une puissance de 2.
+```
+
+> Voir [isPowerOfTwo.js](isPowerOfTwo.js) pour plus de détails.
+
+#### Additionneur complet
+
+Cette méthode ajoute deux nombres entiers à l'aide d'opérateurs bit à bit.
+
+Elle implémente un [additionneur](https://fr.wikipedia.org/wiki/Additionneur)
+simulant un circuit électronique logique,
+pour additionner deux entiers de 32 bits,
+sous la forme « complément à deux ».
+Elle utilise la logique booléenne pour couvrir tous les cas possibles
+d'ajout de deux bits donnés:
+avec et sans retenue de l'ajout de l'étape précédente la moins significative.
+
+Légende:
+
+- `A`: Nombre `A`
+- `B`: Nombre `B`
+- `ai`: ième bit du nombre `A`
+- `bi`: ième bit du nombre `B`
+- `carryIn`: un bit retenu de la précédente étape la moins significative
+- `carryOut`: un bit retenu pour la prochaine étape la plus significative
+- `bitSum`: La somme de `ai`, `bi`, et `carryIn`
+- `resultBin`: Le résultat complet de l'ajout de l'étape actuelle avec toutes les étapes moins significatives (en binaire)
+- `resultDec`: Le résultat complet de l'ajout de l'étape actuelle avec toutes les étapes moins significatives (en decimal)
+
+```
+A = 3: 011
+B = 6: 110
+┌──────┬────┬────┬───────┬────────┬───────┬────────┬─────────┐
+│ bit │ ai │ bi │ carryIn │ carryOut │ bitSum │ resultBin │ resultDec │
+├──────┼────┼────┼───────┼────────┼───────┼────────┼─────────┤
+│ 0 │ 1 │ 0 │ 0 │ 0 │ 1 │ 1 │ 1 │
+│ 1 │ 1 │ 1 │ 0 │ 1 │ 0 │ 01 │ 1 │
+│ 2 │ 0 │ 1 │ 1 │ 1 │ 0 │ 001 │ 1 │
+│ 3 │ 0 │ 0 │ 1 │ 0 │ 1 │ 1001 │ 9 │
+└──────┴────┴────┴───────┴────────┴───────┴────────┴─────────┘
+```
+
+> Voir [fullAdder.js](fullAdder.js) pour plus de détails.
+> Voir [Full Adder on YouTube](https://www.youtube.com/watch?v=wvJc9CZcvBc&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8).
+
+## Références
+
+- [Bit Manipulation on YouTube](https://www.youtube.com/watch?v=NLKQEOgBAnw&t=0s&index=28&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
+- [Negative Numbers in binary on YouTube](https://www.youtube.com/watch?v=4qH4unVtJkE&t=0s&index=30&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
+- [Bit Hacks on stanford.edu](https://graphics.stanford.edu/~seander/bithacks.html)
diff --git a/src/algorithms/math/bits/README.md b/src/algorithms/math/bits/README.md
index f4eca24471..7c0bac48d7 100644
--- a/src/algorithms/math/bits/README.md
+++ b/src/algorithms/math/bits/README.md
@@ -1,10 +1,13 @@
# Bit Manipulation
+_Read this in other languages:_
+[français](README.fr-FR.md).
+
#### Get Bit
This method shifts the relevant bit to the zeroth position.
Then we perform `AND` operation with one which has bit
-pattern like `0001`. This clears all bits from the original
+pattern like `0001`. This clears all bits from the original
number except the relevant one. If the relevant bit is one,
the result is `1`, otherwise the result is `0`.
@@ -53,7 +56,7 @@ isEven: true
#### isPositive
-This method determines if the number is positive. It is based on the fact that all positive
+This method determines if the number is positive. It is based on the fact that all positive
numbers have their leftmost bit to be set to `0`. However, if the number provided is zero
or negative zero, it should still return `false`.
@@ -230,12 +233,13 @@ Number: 9 = (10 - 1) = 0b01001
This method adds up two integer numbers using bitwise operators.
-It implements [full adder](https://en.wikipedia.org/wiki/Adder_(electronics))
+It implements [full adder]()
electronics circuit logic to sum two 32-bit integers in two's complement format.
It's using the boolean logic to cover all possible cases of adding two input bits:
with and without a "carry bit" from adding the previous less-significant stage.
Legend:
+
- `A`: Number `A`
- `B`: Number `B`
- `ai`: ith bit of number `A`
diff --git a/src/algorithms/math/complex-number/README.fr-FR.md b/src/algorithms/math/complex-number/README.fr-FR.md
new file mode 100644
index 0000000000..0e42a484d4
--- /dev/null
+++ b/src/algorithms/math/complex-number/README.fr-FR.md
@@ -0,0 +1,237 @@
+# Nombre complexe
+
+_Read this in other languages:_
+[english](README.md).
+
+Un **nombre complexe** est un nombre qui peut s'écrire sous la forme
+`a + b * i`, tels que `a` et `b` sont des nombres réels,
+et `i` est la solution de l'équation `x^2 = −1`.
+Du fait qu'aucun _nombre réel_ ne statisfait l'équation,
+`i` est appellé _nombre imaginaire_. Étant donné le nombre complexe `a + b * i`,
+`a` est appellé _partie réelle_, et `b`, _partie imaginaire_.
+
+
+
+Un nombre complexe est donc la combinaison
+d'un nombre réel et d'un nombre imaginaire :
+
+
+
+En géométrie, les nombres complexes étendent le concept
+de ligne de nombres sur une dimension à un _plan complexe à deux dimensions_
+en utilisant l'axe horizontal pour lepartie réelle
+et l'axe vertical pour la partie imaginaire. Le nombre complexe `a + b * i`
+peut être identifié avec le point `(a, b)` dans le plan complexe.
+
+Un nombre complexe dont la partie réelle est zéro est dit _imaginaire pur_;
+les points pour ces nombres se trouvent sur l'axe vertical du plan complexe.
+Un nombre complexe dont la partie imaginaire est zéro
+peut être considéré comme un _nombre réel_; son point
+se trouve sur l'axe horizontal du plan complexe.
+
+| Nombre complexe | Partie réelle | partie imaginaire | |
+| :-------------- | :-----------: | :---------------: | ---------------- |
+| 3 + 2i | 3 | 2 | |
+| 5 | 5 | **0** | Purely Real |
+| −6i | **0** | -6 | Purely Imaginary |
+
+A complex number can be visually represented as a pair of numbers `(a, b)` forming
+a vector on a diagram called an _Argand diagram_, representing the _complex plane_.
+`Re` is the real axis, `Im` is the imaginary axis, and `i` satisfies `i^2 = −1`.
+
+Un nombre complexe peut être représenté visuellement comme une paire de nombres
+`(a, b)` formant un vecteur sur un diagramme appelé _diagramme d'Argand_,
+représentant le _plan complexe_.
+_Re_ est l'axe réel, _Im_ est l'axe imaginaire et `i` satisfait `i^2 = −1`.
+
+
+
+> Complexe ne veut pas dire compliqué. Cela signifie simplement que
+> les deux types de nombres, réels et imaginaires, forment ensemble un complexe
+> comme on le dirait d'un complexe de bâtiments (bâtiments réunis).
+
+## Forme polaire
+
+Une manière de définir un point `P` dans le plan complexe, autre que d'utiliser
+les coordonnées x et y, consiste à utiliser la distance entre le point `O`, le point
+dont les coordonnées sont `(0, 0)` (l'origine), et l'angle sous-tendu
+entre l'axe réel positif et le segment de droite `OP` dans le sens antihoraire.
+Cette idée conduit à la forme polaire des nombres complexes.
+
+
+
+The _valeur absolue_ (ou module) d'un nombre complexe `z = x + yi` est:
+
+
+
+L'argument de `z` (parfois appelé « phase » ou « amplitude ») est l'angle
+du rayon `OP` avec l'axe des réels positifs, et s'écrit `arg(z)`. Comme
+avec le module, l'argument peut être trouvé à partir de la forme rectangulaire `x + yi`:
+
+
+
+Ensemble, `r` et`φ` donnent une autre façon de représenter les nombres complexes, la
+forme polaire, car la combinaison du module et de l'argument suffit à indiquer la
+position d'un point sur le plan. Obtenir les coordonnées du rectangle d'origine
+à partir de la forme polaire se fait par la formule appelée forme trigonométrique :
+
+
+
+En utilisant la formule d'Euler, cela peut être écrit comme suit:
+
+
+
+## Opérations de base
+
+### Addition
+
+Pour ajouter deux nombres complexes, nous ajoutons chaque partie séparément :
+
+```text
+(a + b * i) + (c + d * i) = (a + c) + (b + d) * i
+```
+
+**Exemple**
+
+```text
+(3 + 5i) + (4 − 3i) = (3 + 4) + (5 − 3)i = 7 + 2i
+```
+
+Dans un plan complexe, l'addition ressemblera à ceci:
+
+
+
+### Soustraction
+
+Pour soustraire deux nombres complexes, on soustrait chaque partie séparément :
+
+```text
+(a + b * i) - (c + d * i) = (a - c) + (b - d) * i
+```
+
+**Exemple**
+
+```text
+(3 + 5i) - (4 − 3i) = (3 - 4) + (5 + 3)i = -1 + 8i
+```
+
+### Multiplication
+
+Pour multiplier les nombres complexes, chaque partie du premier nombre complexe est multipliée
+par chaque partie du deuxième nombre complexe:
+
+On peut utiliser le "FOIL" (parfois traduit PEID en français), acronyme de
+**F**irsts (Premiers), **O**uters (Extérieurs), **I**nners (Intérieurs), **L**asts (Derniers)" (
+voir [Binomial Multiplication](ttps://www.mathsisfun.com/algebra/polynomials-multiplying.html) pour plus de détails):
+
+
+
+- Firsts: `a × c`
+- Outers: `a × di`
+- Inners: `bi × c`
+- Lasts: `bi × di`
+
+En général, cela ressemble à:
+
+```text
+(a + bi)(c + di) = ac + adi + bci + bdi^2
+```
+
+Mais il existe aussi un moyen plus rapide !
+
+Utiliser cette loi:
+
+```text
+(a + bi)(c + di) = (ac − bd) + (ad + bc)i
+```
+
+**Exemple**
+
+```text
+(3 + 2i)(1 + 7i)
+= 3×1 + 3×7i + 2i×1+ 2i×7i
+= 3 + 21i + 2i + 14i^2
+= 3 + 21i + 2i − 14 (because i^2 = −1)
+= −11 + 23i
+```
+
+```text
+(3 + 2i)(1 + 7i) = (3×1 − 2×7) + (3×7 + 2×1)i = −11 + 23i
+```
+
+### Conjugués
+
+En mathématiques, le conjugué d'un nombre complexe z
+est le nombre complexe formé de la même partie réelle que z
+mais de partie imaginaire opposée.
+
+Un conjugué vois son signe changer au milieu comme suit:
+
+
+
+Un conjugué est souvent écrit avec un trait suscrit (barre au-dessus):
+
+```text
+______
+5 − 3i = 5 + 3i
+```
+
+Dans un plan complexe, le nombre conjugué sera mirroir par rapport aux axes réels.
+
+
+
+### Division
+
+Le conjugué est utiliser pour aider à la division de nombres complexes
+
+L'astuce est de _multiplier le haut et le bas par le conjugué du bas_.
+
+**Exemple**
+
+```text
+2 + 3i
+------
+4 − 5i
+```
+
+Multiplier le haut et le bas par le conjugué de `4 − 5i`:
+
+```text
+ (2 + 3i) * (4 + 5i) 8 + 10i + 12i + 15i^2
+= ------------------- = ----------------------
+ (4 − 5i) * (4 + 5i) 16 + 20i − 20i − 25i^2
+```
+
+Et puisque `i^2 = −1`, il s'ensuit que:
+
+```text
+ 8 + 10i + 12i − 15 −7 + 22i −7 22
+= ------------------- = -------- = -- + -- * i
+ 16 + 20i − 20i + 25 41 41 41
+
+```
+
+Il existe cependant un moyen plus direct.
+
+Dans l'exemple précédent, ce qui s'est passé en bas était intéressant:
+
+```text
+(4 − 5i)(4 + 5i) = 16 + 20i − 20i − 25i
+```
+
+Les termes du milieu `(20i − 20i)` s'annule! Et pusique `i^2 = −1` on retrouve:
+
+```text
+(4 − 5i)(4 + 5i) = 4^2 + 5^2
+```
+
+Ce qui est vraiment un résultat assez simple. La règle générale est:
+
+```text
+(a + bi)(a − bi) = a^2 + b^2
+```
+
+## Références
+
+- [Wikipedia](https://fr.wikipedia.org/wiki/Nombre_complexe)
+- [Math is Fun](https://www.mathsisfun.com/numbers/complex-numbers.html)
diff --git a/src/algorithms/math/complex-number/README.md b/src/algorithms/math/complex-number/README.md
index 9a591e51e2..7629aad3f0 100644
--- a/src/algorithms/math/complex-number/README.md
+++ b/src/algorithms/math/complex-number/README.md
@@ -1,11 +1,14 @@
# Complex Number
-A **complex number** is a number that can be expressed in the
+_Read this in other languages:_
+[français](README.fr-FR.md).
+
+A **complex number** is a number that can be expressed in the
form `a + b * i`, where `a` and `b` are real numbers, and `i` is a solution of
-the equation `x^2 = −1`. Because no *real number* satisfies this
-equation, `i` is called an *imaginary number*. For the complex
-number `a + b * i`, `a` is called the *real part*, and `b` is called
-the *imaginary part*.
+the equation `x^2 = −1`. Because no _real number_ satisfies this
+equation, `i` is called an _imaginary number_. For the complex
+number `a + b * i`, `a` is called the _real part_, and `b` is called
+the _imaginary part_.

@@ -13,56 +16,56 @@ A Complex Number is a combination of a Real Number and an Imaginary Number:

-Geometrically, complex numbers extend the concept of the one-dimensional number
-line to the *two-dimensional complex plane* by using the horizontal axis for the
-real part and the vertical axis for the imaginary part. The complex
-number `a + b * i` can be identified with the point `(a, b)` in the complex plane.
+Geometrically, complex numbers extend the concept of the one-dimensional number
+line to the _two-dimensional complex plane_ by using the horizontal axis for the
+real part and the vertical axis for the imaginary part. The complex
+number `a + b * i` can be identified with the point `(a, b)` in the complex plane.
-A complex number whose real part is zero is said to be *purely imaginary*; the
+A complex number whose real part is zero is said to be _purely imaginary_; the
points for these numbers lie on the vertical axis of the complex plane. A complex
-number whose imaginary part is zero can be viewed as a *real number*; its point
+number whose imaginary part is zero can be viewed as a _real number_; its point
lies on the horizontal axis of the complex plane.
-| Complex Number | Real Part | Imaginary Part | |
-| :------------- | :-------: | :------------: | --- |
-| 3 + 2i | 3 | 2 | |
-| 5 | 5 | **0** | Purely Real |
-| −6i | **0** | -6 | Purely Imaginary |
+| Complex Number | Real Part | Imaginary Part | |
+| :------------- | :-------: | :------------: | ---------------- |
+| 3 + 2i | 3 | 2 | |
+| 5 | 5 | **0** | Purely Real |
+| −6i | **0** | -6 | Purely Imaginary |
-A complex number can be visually represented as a pair of numbers `(a, b)` forming
-a vector on a diagram called an *Argand diagram*, representing the *complex plane*.
+A complex number can be visually represented as a pair of numbers `(a, b)` forming
+a vector on a diagram called an _Argand diagram_, representing the _complex plane_.
`Re` is the real axis, `Im` is the imaginary axis, and `i` satisfies `i^2 = −1`.

-> Complex does not mean complicated. It means the two types of numbers, real and
-imaginary, together form a complex, just like a building complex (buildings
-joined together).
+> Complex does not mean complicated. It means the two types of numbers, real and
+> imaginary, together form a complex, just like a building complex (buildings
+> joined together).
## Polar Form
-An alternative way of defining a point `P` in the complex plane, other than using
+An alternative way of defining a point `P` in the complex plane, other than using
the x- and y-coordinates, is to use the distance of the point from `O`, the point
-whose coordinates are `(0, 0)` (the origin), together with the angle subtended
-between the positive real axis and the line segment `OP` in a counterclockwise
+whose coordinates are `(0, 0)` (the origin), together with the angle subtended
+between the positive real axis and the line segment `OP` in a counterclockwise
direction. This idea leads to the polar form of complex numbers.

-The *absolute value* (or modulus or magnitude) of a complex number `z = x + yi` is:
+The _absolute value_ (or modulus or magnitude) of a complex number `z = x + yi` is:

The argument of `z` (in many applications referred to as the "phase") is the angle
-of the radius `OP` with the positive real axis, and is written as `arg(z)`. As
+of the radius `OP` with the positive real axis, and is written as `arg(z)`. As
with the modulus, the argument can be found from the rectangular form `x+yi`:

-Together, `r` and `φ` give another way of representing complex numbers, the
-polar form, as the combination of modulus and argument fully specify the
-position of a point on the plane. Recovering the original rectangular
-co-ordinates from the polar form is done by the formula called trigonometric
+Together, `r` and `φ` give another way of representing complex numbers, the
+polar form, as the combination of modulus and argument fully specify the
+position of a point on the plane. Recovering the original rectangular
+co-ordinates from the polar form is done by the formula called trigonometric
form:

@@ -107,7 +110,7 @@ To subtract two complex numbers we subtract each part separately:
### Multiplying
-To multiply complex numbers each part of the first complex number gets multiplied
+To multiply complex numbers each part of the first complex number gets multiplied
by each part of the second complex number:
Just use "FOIL", which stands for "**F**irsts, **O**uters, **I**nners, **L**asts" (
@@ -138,7 +141,7 @@ Use this rule:
**Example**
```text
-(3 + 2i)(1 + 7i)
+(3 + 2i)(1 + 7i)
= 3×1 + 3×7i + 2i×1+ 2i×7i
= 3 + 21i + 2i + 14i^2
= 3 + 21i + 2i − 14 (because i^2 = −1)
@@ -164,7 +167,7 @@ ______
5 − 3i = 5 + 3i
```
-On the complex plane the conjugate number will be mirrored against real axes.
+On the complex plane the conjugate number will be mirrored against real axes.

@@ -172,7 +175,7 @@ On the complex plane the conjugate number will be mirrored against real axes.
The conjugate is used to help complex division.
-The trick is to *multiply both top and bottom by the conjugate of the bottom*.
+The trick is to _multiply both top and bottom by the conjugate of the bottom_.
**Example**
@@ -207,7 +210,7 @@ In the previous example, what happened on the bottom was interesting:
(4 − 5i)(4 + 5i) = 16 + 20i − 20i − 25i
```
-The middle terms `(20i − 20i)` cancel out! Also `i^2 = −1` so we end up with this:
+The middle terms `(20i − 20i)` cancel out! Also `i^2 = −1` so we end up with this:
```text
(4 − 5i)(4 + 5i) = 4^2 + 5^2
diff --git a/src/algorithms/math/euclidean-algorithm/README.fr-FR.md b/src/algorithms/math/euclidean-algorithm/README.fr-FR.md
new file mode 100644
index 0000000000..75b6a90b88
--- /dev/null
+++ b/src/algorithms/math/euclidean-algorithm/README.fr-FR.md
@@ -0,0 +1,49 @@
+# Algorithme d'Euclide
+
+_Read this in other languages:_
+[english](README.md).
+
+En mathématiques, l'algorithme d'Euclide est un algorithme qui calcule le plus grand commun diviseur (PGCD) de deux entiers, c'est-à-dire le plus grand entier qui divise les deux entiers, en laissant un reste nul. L'algorithme ne connaît pas la factorisation de ces deux nombres.
+
+Le PGCD de deux entiers relatifs est égal au PGCD de leurs valeurs absolues : de ce fait, on se restreint dans cette section aux entiers positifs. L'algorithme part du constat suivant : le PGCD de deux nombres n'est pas changé si on remplace le plus grand d'entre eux par leur différence. Autrement dit, `pgcd(a, b) = pgcd(b, a - b)`. Par exemple, le PGCD de `252` et `105` vaut `21` (en effet, `252 = 21 × 12` and `105 = 21 × 5`), mais c'est aussi le PGCD de `252 - 105 = 147` et `105`. Ainsi, comme le remplacement de ces nombres diminue strictement le plus grand d'entre eux, on peut continuer le processus, jusqu'à obtenir deux nombres égaux.
+
+En inversant les étapes, le PGCD peut être exprimé comme une somme de
+les deux nombres originaux, chacun étant multiplié
+par un entier positif ou négatif, par exemple `21 = 5 × 105 + (-2) × 252`.
+Le fait que le PGCD puisse toujours être exprimé de cette manière est
+connue sous le nom de Théorème de Bachet-Bézout.
+
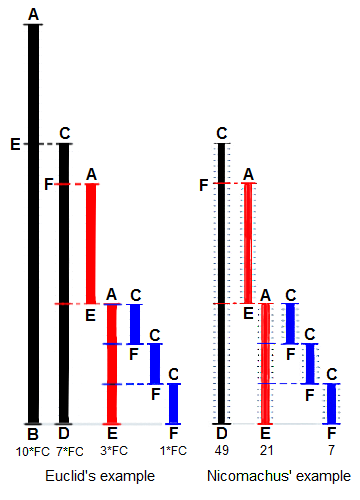
+
+
+La Méthode d'Euclide pour trouver le plus grand diviseur commun (PGCD)
+de deux longueurs de départ`BA` et `DC`, toutes deux définies comme étant
+multiples d'une longueur commune. La longueur `DC` étant
+plus courte, elle est utilisée pour « mesurer » `BA`, mais une seule fois car
+le reste `EA` est inférieur à `DC`. `EA` mesure maintenant (deux fois)
+la longueur la plus courte `DC`, le reste `FC` étant plus court que `EA`.
+Alors `FC` mesure (trois fois) la longueur `EA`. Parce qu'il y a
+pas de reste, le processus se termine par `FC` étant le « PGCD ».
+À droite, l'exemple de Nicomaque de Gérase avec les nombres `49` et `21`
+ayan un PGCD de `7` (dérivé de Heath 1908: 300).
+
+
+
+Un de rectangle de dimensions `24 par 60` peux se carreler en carrés de `12 par 12`,
+puisque `12` est le PGCD ed `24` et `60`. De façon générale,
+un rectangle de dimension `a par b` peut se carreler en carrés
+de côté `c`, seulement si `c` est un diviseur commun de `a` et `b`.
+
+
+
+Animation basée sur la soustraction via l'algorithme euclidien.
+Le rectangle initial a les dimensions `a = 1071` et `b = 462`.
+Des carrés de taille `462 × 462` y sont placés en laissant un
+rectangle de `462 × 147`. Ce rectangle est carrelé avec des
+carrés de `147 × 147` jusqu'à ce qu'un rectangle de `21 × 147` soit laissé,
+qui à son tour estcarrelé avec des carrés `21 × 21`,
+ne laissant aucune zone non couverte.
+La plus petite taille carrée, `21`, est le PGCD de `1071` et `462`.
+
+## References
+
+[Wikipedia](https://fr.wikipedia.org/wiki/Algorithme_d%27Euclide)
diff --git a/src/algorithms/math/euclidean-algorithm/README.md b/src/algorithms/math/euclidean-algorithm/README.md
index a7276fd53c..89af03b15e 100644
--- a/src/algorithms/math/euclidean-algorithm/README.md
+++ b/src/algorithms/math/euclidean-algorithm/README.md
@@ -1,55 +1,58 @@
# Euclidean algorithm
-In mathematics, the Euclidean algorithm, or Euclid's algorithm,
-is an efficient method for computing the greatest common divisor
-(GCD) of two numbers, the largest number that divides both of
+_Read this in other languages:_
+[français](README.fr-FR.md).
+
+In mathematics, the Euclidean algorithm, or Euclid's algorithm,
+is an efficient method for computing the greatest common divisor
+(GCD) of two numbers, the largest number that divides both of
them without leaving a remainder.
-The Euclidean algorithm is based on the principle that the
-greatest common divisor of two numbers does not change if
-the larger number is replaced by its difference with the
-smaller number. For example, `21` is the GCD of `252` and
-`105` (as `252 = 21 × 12` and `105 = 21 × 5`), and the same
-number `21` is also the GCD of `105` and `252 − 105 = 147`.
-Since this replacement reduces the larger of the two numbers,
-repeating this process gives successively smaller pairs of
-numbers until the two numbers become equal.
-When that occurs, they are the GCD of the original two numbers.
-
-By reversing the steps, the GCD can be expressed as a sum of
-the two original numbers each multiplied by a positive or
-negative integer, e.g., `21 = 5 × 105 + (−2) × 252`.
-The fact that the GCD can always be expressed in this way is
+The Euclidean algorithm is based on the principle that the
+greatest common divisor of two numbers does not change if
+the larger number is replaced by its difference with the
+smaller number. For example, `21` is the GCD of `252` and
+`105` (as `252 = 21 × 12` and `105 = 21 × 5`), and the same
+number `21` is also the GCD of `105` and `252 − 105 = 147`.
+Since this replacement reduces the larger of the two numbers,
+repeating this process gives successively smaller pairs of
+numbers until the two numbers become equal.
+When that occurs, they are the GCD of the original two numbers.
+
+By reversing the steps, the GCD can be expressed as a sum of
+the two original numbers each multiplied by a positive or
+negative integer, e.g., `21 = 5 × 105 + (−2) × 252`.
+The fact that the GCD can always be expressed in this way is
known as Bézout's identity.

-Euclid's method for finding the greatest common divisor (GCD)
-of two starting lengths `BA` and `DC`, both defined to be
-multiples of a common "unit" length. The length `DC` being
-shorter, it is used to "measure" `BA`, but only once because
-remainder `EA` is less than `DC`. EA now measures (twice)
-the shorter length `DC`, with remainder `FC` shorter than `EA`.
-Then `FC` measures (three times) length `EA`. Because there is
-no remainder, the process ends with `FC` being the `GCD`.
-On the right Nicomachus' example with numbers `49` and `21`
+Euclid's method for finding the greatest common divisor (GCD)
+of two starting lengths `BA` and `DC`, both defined to be
+multiples of a common "unit" length. The length `DC` being
+shorter, it is used to "measure" `BA`, but only once because
+remainder `EA` is less than `DC`. EA now measures (twice)
+the shorter length `DC`, with remainder `FC` shorter than `EA`.
+Then `FC` measures (three times) length `EA`. Because there is
+no remainder, the process ends with `FC` being the `GCD`.
+On the right Nicomachus' example with numbers `49` and `21`
resulting in their GCD of `7` (derived from Heath 1908:300).

-A `24-by-60` rectangle is covered with ten `12-by-12` square
-tiles, where `12` is the GCD of `24` and `60`. More generally,
-an `a-by-b` rectangle can be covered with square tiles of
+A `24-by-60` rectangle is covered with ten `12-by-12` square
+tiles, where `12` is the GCD of `24` and `60`. More generally,
+an `a-by-b` rectangle can be covered with square tiles of
side-length `c` only if `c` is a common divisor of `a` and `b`.

-Subtraction-based animation of the Euclidean algorithm.
-The initial rectangle has dimensions `a = 1071` and `b = 462`.
-Squares of size `462×462` are placed within it leaving a
-`462×147` rectangle. This rectangle is tiled with `147×147`
-squares until a `21×147` rectangle is left, which in turn is
-tiled with `21×21` squares, leaving no uncovered area.
+Subtraction-based animation of the Euclidean algorithm.
+The initial rectangle has dimensions `a = 1071` and `b = 462`.
+Squares of size `462×462` are placed within it leaving a
+`462×147` rectangle. This rectangle is tiled with `147×147`
+squares until a `21×147` rectangle is left, which in turn is
+tiled with `21×21` squares, leaving no uncovered area.
The smallest square size, `21`, is the GCD of `1071` and `462`.
## References
diff --git a/src/algorithms/math/factorial/README.fr-FR.md b/src/algorithms/math/factorial/README.fr-FR.md
new file mode 100644
index 0000000000..aa092c1b78
--- /dev/null
+++ b/src/algorithms/math/factorial/README.fr-FR.md
@@ -0,0 +1,35 @@
+# Factorielle
+
+_Lisez ceci dans d'autres langues:_
+[english](README.md), [_简体中文_](README.zh-CN.md).
+
+En mathématiques, la factorielle d'un entier naturel `n`,
+notée avec un point d'exclamation `n!`, est le produit des nombres entiers
+strictement positifs inférieurs ou égaux à n. Par exemple:
+
+```
+5! = 5 * 4 * 3 * 2 * 1 = 120
+```
+
+| n | n! |
+| --- | ----------------: |
+| 0 | 1 |
+| 1 | 1 |
+| 2 | 2 |
+| 3 | 6 |
+| 4 | 24 |
+| 5 | 120 |
+| 6 | 720 |
+| 7 | 5 040 |
+| 8 | 40 320 |
+| 9 | 362 880 |
+| 10 | 3 628 800 |
+| 11 | 39 916 800 |
+| 12 | 479 001 600 |
+| 13 | 6 227 020 800 |
+| 14 | 87 178 291 200 |
+| 15 | 1 307 674 368 000 |
+
+## References
+
+[Wikipedia](https://fr.wikipedia.org/wiki/Factorielle)
diff --git a/src/algorithms/math/factorial/README.md b/src/algorithms/math/factorial/README.md
index bd5df77020..107b55a3d3 100644
--- a/src/algorithms/math/factorial/README.md
+++ b/src/algorithms/math/factorial/README.md
@@ -1,34 +1,34 @@
# Factorial
_Read this in other languages:_
-[_简体中文_](README.zh-CN.md),
+[_简体中文_](README.zh-CN.md), [français](README.fr-FR.md).
-In mathematics, the factorial of a non-negative integer `n`,
-denoted by `n!`, is the product of all positive integers less
+In mathematics, the factorial of a non-negative integer `n`,
+denoted by `n!`, is the product of all positive integers less
than or equal to `n`. For example:
```
5! = 5 * 4 * 3 * 2 * 1 = 120
```
-| n | n! |
-| ----- | --------------------------: |
-| 0 | 1 |
-| 1 | 1 |
-| 2 | 2 |
-| 3 | 6 |
-| 4 | 24 |
-| 5 | 120 |
-| 6 | 720 |
-| 7 | 5 040 |
-| 8 | 40 320 |
-| 9 | 362 880 |
-| 10 | 3 628 800 |
-| 11 | 39 916 800 |
-| 12 | 479 001 600 |
-| 13 | 6 227 020 800 |
-| 14 | 87 178 291 200 |
-| 15 | 1 307 674 368 000 |
+| n | n! |
+| --- | ----------------: |
+| 0 | 1 |
+| 1 | 1 |
+| 2 | 2 |
+| 3 | 6 |
+| 4 | 24 |
+| 5 | 120 |
+| 6 | 720 |
+| 7 | 5 040 |
+| 8 | 40 320 |
+| 9 | 362 880 |
+| 10 | 3 628 800 |
+| 11 | 39 916 800 |
+| 12 | 479 001 600 |
+| 13 | 6 227 020 800 |
+| 14 | 87 178 291 200 |
+| 15 | 1 307 674 368 000 |
## References
diff --git a/src/algorithms/math/fast-powering/README.fr-FR.md b/src/algorithms/math/fast-powering/README.fr-FR.md
new file mode 100644
index 0000000000..ba44244cc8
--- /dev/null
+++ b/src/algorithms/math/fast-powering/README.fr-FR.md
@@ -0,0 +1,73 @@
+# Algorithme d'exponentiation rapide
+
+_Read this in other languages:_
+[english](README.md).
+
+En algèbre, une **puissance** d'un nombre est le résultat de la multiplication répétée de ce nombre avec lui-même.
+
+Elle est souvent notée en assortissant le nombre d'un entier, typographié en exposant, qui indique le nombre de fois qu'apparaît le nombre comme facteur dans cette multiplication.
+
+
+
+## Implémentation « naïve »
+
+Comment trouver `a` élevé à la puissance `b` ?
+
+On multiplie `a` avec lui-même, `b` nombre de fois.
+Ainsi, `a^b = a * a * a * ... * a` (`b` occurrences de `a`).
+
+Cette opération aura un complexité linéaire, notée `O(n)`,
+car la multiplication aura lieu exactement `n` fois.
+
+## Algorithme d'exponentiation rapide
+
+Peut-on faire mieux que cette implémentation naïve?
+Oui, on peut réduire le nombre de puissance à un complexité de `O(log(n))`.
+
+Cet algorithme utilise l'approche « diviser pour mieux régner »
+pour calculer cette puissance.
+En l'état, cet algorithme fonctionne pour deux entiers positifs `X` et `Y`.
+
+L'idée derrière cet algorithme est basée sur l'observation suivante.
+
+Lorsque `Y` est **pair**:
+
+```text
+X^Y = X^(Y/2) * X^(Y/2)
+```
+
+Lorsque `Y` est **impair**:
+
+```text
+X^Y = X^(Y//2) * X^(Y//2) * X
+où Y//2 est le résultat de la division entière de Y par 2.
+```
+
+**Par exemple**
+
+```text
+2^4 = (2 * 2) * (2 * 2) = (2^2) * (2^2)
+```
+
+```text
+2^5 = (2 * 2) * (2 * 2) * 2 = (2^2) * (2^2) * (2)
+```
+
+Ainsi, puisqu'à chaque étape on doits calculer
+deux fois la même puissance `X ^ (Y / 2)`,
+on peut optimiser en l'enregistrant dans une variable intermédiaire
+pour éviter son calcul en double.
+
+**Complexité en temps**
+
+Comme à chaque itération nous réduisons la puissance de moitié,
+nous appelons récursivement la fonction `log(n)` fois. Le complexité de temps de cet algorithme est donc réduite à:
+
+```text
+O(log(n))
+```
+
+## Références
+
+- [YouTube](https://www.youtube.com/watch?v=LUWavfN9zEo&index=80&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&t=0s)
+- [Wikipedia](https://fr.wikipedia.org/wiki/Exponentiation_rapide)
diff --git a/src/algorithms/math/fast-powering/README.md b/src/algorithms/math/fast-powering/README.md
index 13745afa04..2c2619d2ef 100644
--- a/src/algorithms/math/fast-powering/README.md
+++ b/src/algorithms/math/fast-powering/README.md
@@ -1,6 +1,9 @@
# Fast Powering Algorithm
-**The power of a number** says how many times to use the number in a
+_Read this in other languages:_
+[français](README.fr-FR.md).
+
+**The power of a number** says how many times to use the number in a
multiplication.
It is written as a small number to the right and above the base number.
@@ -11,7 +14,7 @@ It is written as a small number to the right and above the base number.
How to find `a` raised to the power `b`?
-We multiply `a` to itself, `b` times. That
+We multiply `a` to itself, `b` times. That
is, `a^b = a * a * a * ... * a` (`b` occurrences of `a`).
This operation will take `O(n)` time since we need to do multiplication operation
@@ -20,9 +23,9 @@ exactly `n` times.
## Fast Power Algorithm
Can we do better than naive algorithm does? Yes we may solve the task of
- powering in `O(log(n))` time.
+powering in `O(log(n))` time.
-The algorithm uses divide and conquer approach to compute power. Currently the
+The algorithm uses divide and conquer approach to compute power. Currently the
algorithm work for two positive integers `X` and `Y`.
The idea behind the algorithm is based on the fact that:
@@ -30,7 +33,7 @@ The idea behind the algorithm is based on the fact that:
For **even** `Y`:
```text
-X^Y = X^(Y/2) * X^(Y/2)
+X^Y = X^(Y/2) * X^(Y/2)
```
For **odd** `Y`:
@@ -50,17 +53,17 @@ where Y//2 is result of division of Y by 2 without reminder.
2^5 = (2 * 2) * (2 * 2) * 2 = (2^2) * (2^2) * (2)
```
-Now, since on each step we need to compute the same `X^(Y/2)` power twice we may optimise
-it by saving it to some intermediate variable to avoid its duplicate calculation.
+Now, since on each step we need to compute the same `X^(Y/2)` power twice we may optimise
+it by saving it to some intermediate variable to avoid its duplicate calculation.
**Time Complexity**
-Since each iteration we split the power by half then we will call function
+Since each iteration we split the power by half then we will call function
recursively `log(n)` times. This the time complexity of the algorithm is reduced to:
```text
O(log(n))
-```
+```
## References
diff --git a/src/algorithms/math/fibonacci/README.fr-FR.md b/src/algorithms/math/fibonacci/README.fr-FR.md
new file mode 100644
index 0000000000..1321ca24d7
--- /dev/null
+++ b/src/algorithms/math/fibonacci/README.fr-FR.md
@@ -0,0 +1,23 @@
+# Nombre de Fibonacci
+
+_Read this in other languages:_
+[english](README.md).
+
+En mathématiques, la suite de Fibonacci est une suite d'entiers
+dans laquelle chaque terme (après les deux premiers)
+est la somme des deux termes qui le précèdent.
+Les termes de cette suite sont appelés nombres de Fibonacci:
+
+`0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...`
+
+Les carrés de Fibonacci en spirale s'ajustent ensemble pour former une spirale d'or.
+
+
+
+La spirale de Fibonacci: approximation d'une spirale d'or créée en dessinant des arcs de cercle reliant les coins opposés de carrés dans un pavage Fibonacci[4] . Celui-ci utilise des carrés de tailles 1, 1, 2, 3, 5, 8, 13, 21, et 34.
+
+
+
+## References
+
+- [Wikipedia](https://fr.wikipedia.org/wiki/Suite_de_Fibonacci)
diff --git a/src/algorithms/math/fibonacci/README.md b/src/algorithms/math/fibonacci/README.md
index 5efb3543dd..47f571762b 100644
--- a/src/algorithms/math/fibonacci/README.md
+++ b/src/algorithms/math/fibonacci/README.md
@@ -1,8 +1,11 @@
# Fibonacci Number
-In mathematics, the Fibonacci numbers are the numbers in the following
-integer sequence, called the Fibonacci sequence, and characterized by
-the fact that every number after the first two is the sum of the two
+_Read this in other languages:_
+[français](README.fr-FR.md).
+
+In mathematics, the Fibonacci numbers are the numbers in the following
+integer sequence, called the Fibonacci sequence, and characterized by
+the fact that every number after the first two is the sum of the two
preceding ones:
`0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...`
diff --git a/src/algorithms/math/fourier-transform/README.fr-FR.md b/src/algorithms/math/fourier-transform/README.fr-FR.md
new file mode 100644
index 0000000000..0d345164c7
--- /dev/null
+++ b/src/algorithms/math/fourier-transform/README.fr-FR.md
@@ -0,0 +1,135 @@
+# Transformation de Fourier
+
+_Read this in other languages:_
+[english](README.md).
+
+## Définitions
+
+La transformation de Fourier (**ℱ**) est une opération qui transforme
+une fonction intégrable sur ℝ en une autre fonction,
+décrivant le spectre fréquentiel de cette dernière
+
+La **Transformée de Fourier Discrète** (**TFD**) convertit une séquence finie d'échantillons également espacés d'une fonction, dans une séquence de même longueur d'échantillons, également espacés de la Transformée de Fourier à temps discret (TFtd), qui est une fonction complexe de la fréquence.
+L'intervalle auquel le TFtd est échantillonné est l'inverse de la durée de la séquence d'entrée.
+Une TFD inverse est une série de Fourier, utilisant les échantillons TFtd comme coefficients de sinusoïdes complexes aux fréquences TFtd correspondantes. Elle a les mêmes valeurs d'échantillonnage que la
+séquence d'entrée originale. On dit donc que la TFD est une représentation du domaine fréquentiel
+de la séquence d'entrée d'origine. Si la séquence d'origine couvre toutes les
+valeurs non nulles d'une fonction, sa TFtd est continue (et périodique), et la TFD fournit
+les échantillons discrets d'une fenêtre. Si la séquence d'origine est un cycle d'une fonction périodique, la TFD fournit toutes les valeurs non nulles d'une fenêtre TFtd.
+
+Transformée de Fourier Discrète converti une séquence de `N` nombres complexes:
+
+{xn} = x0, x1, x2 ..., xN-1
+
+en une atre séquence de nombres complexes::
+
+{Xk} = X0, X1, X2 ..., XN-1
+
+décrite par:
+
+
+
+The **Transformée de Fourier à temps discret** (**TFtd**) est une forme d'analyse de Fourier
+qui s'applique aux échantillons uniformément espacés d'une fonction continue. Le terme "temps discret" fait référence au fait que la transformée fonctionne sur des données discrètes
+(échantillons) dont l'intervalle a souvent des unités de temps.
+À partir des seuls échantillons, elle produit une fonction de fréquence qui est une somme périodique de la
+Transformée de Fourier continue de la fonction continue d'origine.
+
+A **Transformation de Fourier rapide** (**FFT** pour Fast Fourier Transform) est un algorithme de calcul de la transformation de Fourier discrète (TFD). Il est couramment utilisé en traitement numérique du signal pour transformer des données discrètes du domaine temporel dans le domaine fréquentiel, en particulier dans les oscilloscopes numériques (les analyseurs de spectre utilisant plutôt des filtres analogiques, plus précis). Son efficacité permet de réaliser des filtrages en modifiant le spectre et en utilisant la transformation inverse (filtre à réponse impulsionnelle finie).
+
+Cette transformation peut être illustée par la formule suivante. Sur la période de temps mesurée
+dans le diagramme, le signal contient 3 fréquences dominantes distinctes.
+
+Vue d'un signal dans le domaine temporel et fréquentiel:
+
+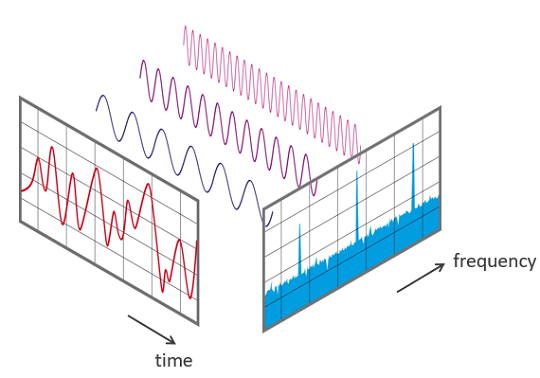
+
+An FFT algorithm computes the discrete Fourier transform (DFT) of a sequence, or
+its inverse (IFFT). Fourier analysis converts a signal from its original domain
+to a representation in the frequency domain and vice versa. An FFT rapidly
+computes such transformations by factorizing the DFT matrix into a product of
+sparse (mostly zero) factors. As a result, it manages to reduce the complexity of
+computing the DFT from O(n2), which arises if one simply applies the
+definition of DFT, to O(n log n), where n is the data size.
+
+Un algorithme FFT calcule la Transformée de Fourier discrète (TFD) d'une séquence, ou
+son inverse (IFFT). L'analyse de Fourier convertit un signal de son domaine d'origine
+en une représentation dans le domaine fréquentiel et vice versa. Une FFT
+calcule rapidement ces transformations en factorisant la matrice TFD en un produit de
+facteurs dispersés (généralement nuls). En conséquence, il parvient à réduire la complexité de
+calcul de la TFD de O (n 2 ), qui survient si l'on applique simplement la
+définition de TFD, à O (n log n), où n est la taille des données.
+
+Voici une analyse de Fourier discrète d'une somme d'ondes cosinus à 10, 20, 30, 40,
+et 50 Hz:
+
+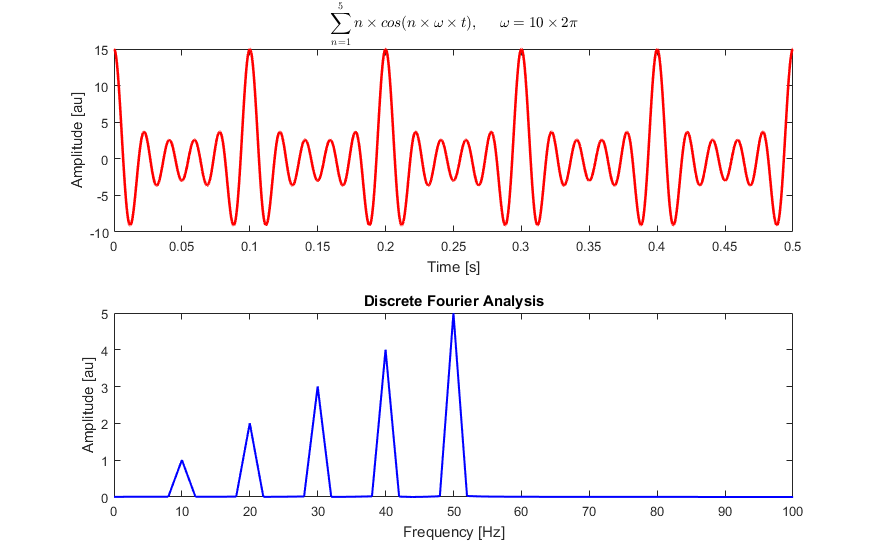
+
+## Explanation
+
+La Transformée de Fourier est l'une des connaissances les plus importante jamais découverte. Malheureusement, le
+son sens est enfoui dans des équations denses::
+
+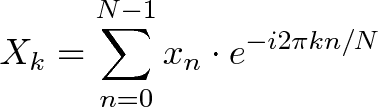
+
+et
+
+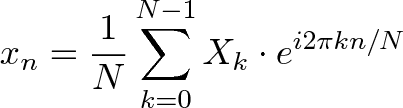
+
+Plutôt que se noyer dans les symboles, faisons en premier lieu l'expérience de l'idée principale. Voici une métaphore en français simple:
+
+- _Que fait la transformée de Fourier ?_ A partir d'un smoothie, elle trouve sa recette.
+- _Comment ?_ Elle passe le smoothie dans un filtre pour en extraire chaque ingrédient.
+- _Pourquoi ?_ Les recettes sont plus faciles à analyser, comparer et modifier que le smoothie lui-même.
+- _Comment récupérer le smoothie ?_ Re-mélanger les ingrédients.
+
+**Pensez en cercles, pas seulement en sinusoïdes**
+
+La transformée de Fourier concerne des trajectoires circulaires (pas les sinusoïdes 1-d)
+et la formuled'Euler est une manière intelligente d'en générer une:
+
+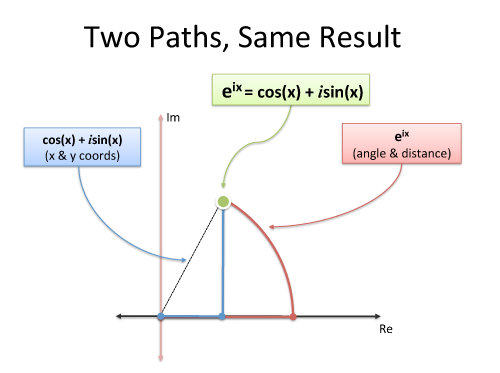
+
+Doit-on utiliser des exposants imaginaires pour se déplacer en cercle ? Non. Mais c'est pratique
+et compact. Et bien sûr, nous pouvons décrire notre chemin comme un mouvement coordonné en deux
+dimensions (réelle et imaginaire), mais n'oubliez pas la vue d'ensemble: nous sommes juste
+en déplacement dans un cercle.
+
+**À la découverte de la transformation complète**
+
+L'idée générale: notre signal n'est qu'un tas de pics de temps, d'instant T ! Si nous combinons les
+recettes pour chaque pic de temps, nous devrions obtenir la recette du signal complet.
+
+La transformée de Fourier construit cette recette fréquence par fréquence:
+
+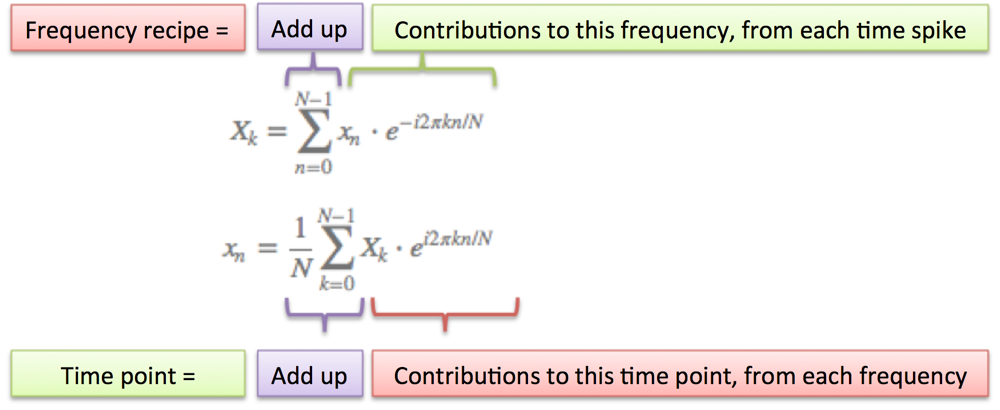
+
+Quelques notes
+
+- N = nombre d'échantillons de temps dont nous disposons
+- n = échantillon actuellement étudié (0 ... N-1)
+- xn = valeur du signal au temps n
+- k = fréquence actuellement étudiée (0 Hertz up to N-1 Hertz)
+- Xk = quantité de fréquence k dans le signal (amplitude et phase, un nombre complexe)
+- Le facteur 1 / N est généralement déplacé vers la transformée inverse (passant des fréquences au temps). Ceci est autorisé, bien que je préfère 1 / N dans la transformation directe car cela donne les tailles réelles des pics de temps. Vous pouvez être plus ambitieux et utiliser 1 / racine carrée de (N) sur les deux transformations (aller en avant et en arrière crée le facteur 1 / N).
+- n/N est le pourcentage du temps que nous avons passé. 2 _ pi _ k est notre vitesse en radians/s. e ^ -ix est notre chemin circulaire vers l'arrière. La combinaison est la distance parcourue, pour cette vitesse et ce temps.
+- Les équations brutes de la transformée de Fourier consiste simplement à "ajouter les nombres complexes". De nombreux langages de programmation ne peuvent pas gérer directement les nombres complexes, on converti donc tout en coordonnées rectangulaires, pour les ajouter.
+
+Stuart Riffle a une excellente interprétation de la transformée de Fourier:
+
+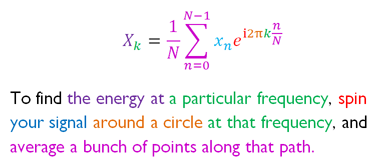
+
+## Références
+
+- Wikipedia
+
+ - [TF](https://fr.wikipedia.org/wiki/Transformation_de_Fourier)
+ - [TFD](https://fr.wikipedia.org/wiki/Transformation_de_Fourier_discr%C3%A8te)
+ - [FFT](https://fr.wikipedia.org/wiki/Transformation_de_Fourier_rapide)
+ - [TFtd (en anglais)](https://en.wikipedia.org/wiki/Discrete-time_Fourier_transform)
+
+- en Anglais
+ - [An Interactive Guide To The Fourier Transform](https://betterexplained.com/articles/an-interactive-guide-to-the-fourier-transform/)
+ - [DFT on YouTube by Better Explained](https://www.youtube.com/watch?v=iN0VG9N2q0U&t=0s&index=77&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
+ - [FT on YouTube by 3Blue1Brown](https://www.youtube.com/watch?v=spUNpyF58BY&t=0s&index=76&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
+ - [FFT on YouTube by Simon Xu](https://www.youtube.com/watch?v=htCj9exbGo0&index=78&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&t=0s)
diff --git a/src/algorithms/math/fourier-transform/README.md b/src/algorithms/math/fourier-transform/README.md
index b1785d725f..f7969ddd5c 100644
--- a/src/algorithms/math/fourier-transform/README.md
+++ b/src/algorithms/math/fourier-transform/README.md
@@ -1,26 +1,29 @@
# Fourier Transform
+_Read this in other languages:_
+[français](README.fr-FR.md).
+
## Definitions
-The **Fourier Transform** (**FT**) decomposes a function of time (a signal) into
-the frequencies that make it up, in a way similar to how a musical chord can be
+The **Fourier Transform** (**FT**) decomposes a function of time (a signal) into
+the frequencies that make it up, in a way similar to how a musical chord can be
expressed as the frequencies (or pitches) of its constituent notes.
-The **Discrete Fourier Transform** (**DFT**) converts a finite sequence of
-equally-spaced samples of a function into a same-length sequence of
-equally-spaced samples of the discrete-time Fourier transform (DTFT), which is a
-complex-valued function of frequency. The interval at which the DTFT is sampled
-is the reciprocal of the duration of the input sequence. An inverse DFT is a
-Fourier series, using the DTFT samples as coefficients of complex sinusoids at
-the corresponding DTFT frequencies. It has the same sample-values as the original
-input sequence. The DFT is therefore said to be a frequency domain representation
-of the original input sequence. If the original sequence spans all the non-zero
-values of a function, its DTFT is continuous (and periodic), and the DFT provides
-discrete samples of one cycle. If the original sequence is one cycle of a periodic
+The **Discrete Fourier Transform** (**DFT**) converts a finite sequence of
+equally-spaced samples of a function into a same-length sequence of
+equally-spaced samples of the discrete-time Fourier transform (DTFT), which is a
+complex-valued function of frequency. The interval at which the DTFT is sampled
+is the reciprocal of the duration of the input sequence. An inverse DFT is a
+Fourier series, using the DTFT samples as coefficients of complex sinusoids at
+the corresponding DTFT frequencies. It has the same sample-values as the original
+input sequence. The DFT is therefore said to be a frequency domain representation
+of the original input sequence. If the original sequence spans all the non-zero
+values of a function, its DTFT is continuous (and periodic), and the DFT provides
+discrete samples of one cycle. If the original sequence is one cycle of a periodic
function, the DFT provides all the non-zero values of one DTFT cycle.
The Discrete Fourier transform transforms a sequence of `N` complex numbers:
-
+
{xn} = x0, x1, x2 ..., xN-1
into another sequence of complex numbers:
@@ -31,16 +34,16 @@ which is defined by:

-The **Discrete-Time Fourier Transform** (**DTFT**) is a form of Fourier analysis
-that is applicable to the uniformly-spaced samples of a continuous function. The
+The **Discrete-Time Fourier Transform** (**DTFT**) is a form of Fourier analysis
+that is applicable to the uniformly-spaced samples of a continuous function. The
term discrete-time refers to the fact that the transform operates on discrete data
-(samples) whose interval often has units of time. From only the samples, it
-produces a function of frequency that is a periodic summation of the continuous
+(samples) whose interval often has units of time. From only the samples, it
+produces a function of frequency that is a periodic summation of the continuous
Fourier transform of the original continuous function.
A **Fast Fourier Transform** (**FFT**) is an algorithm that samples a signal over
-a period of time (or space) and divides it into its frequency components. These
-components are single sinusoidal oscillations at distinct frequencies each with
+a period of time (or space) and divides it into its frequency components. These
+components are single sinusoidal oscillations at distinct frequencies each with
their own amplitude and phase.
This transformation is illustrated in Diagram below. Over the time period measured
@@ -50,22 +53,22 @@ View of a signal in the time and frequency domain:

-An FFT algorithm computes the discrete Fourier transform (DFT) of a sequence, or
-its inverse (IFFT). Fourier analysis converts a signal from its original domain
-to a representation in the frequency domain and vice versa. An FFT rapidly
-computes such transformations by factorizing the DFT matrix into a product of
-sparse (mostly zero) factors. As a result, it manages to reduce the complexity of
-computing the DFT from O(n2), which arises if one simply applies the
+An FFT algorithm computes the discrete Fourier transform (DFT) of a sequence, or
+its inverse (IFFT). Fourier analysis converts a signal from its original domain
+to a representation in the frequency domain and vice versa. An FFT rapidly
+computes such transformations by factorizing the DFT matrix into a product of
+sparse (mostly zero) factors. As a result, it manages to reduce the complexity of
+computing the DFT from O(n2), which arises if one simply applies the
definition of DFT, to O(n log n), where n is the data size.
-Here a discrete Fourier analysis of a sum of cosine waves at 10, 20, 30, 40,
+Here a discrete Fourier analysis of a sum of cosine waves at 10, 20, 30, 40,
and 50 Hz:

## Explanation
-The Fourier Transform is one of deepest insights ever made. Unfortunately, the
+The Fourier Transform is one of deepest insights ever made. Unfortunately, the
meaning is buried within dense equations:
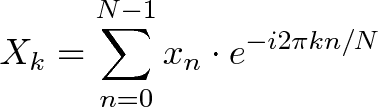
@@ -76,26 +79,26 @@ and
Rather than jumping into the symbols, let's experience the key idea firsthand. Here's a plain-English metaphor:
-- *What does the Fourier Transform do?* Given a smoothie, it finds the recipe.
-- *How?* Run the smoothie through filters to extract each ingredient.
-- *Why?* Recipes are easier to analyze, compare, and modify than the smoothie itself.
-- *How do we get the smoothie back?* Blend the ingredients.
+- _What does the Fourier Transform do?_ Given a smoothie, it finds the recipe.
+- _How?_ Run the smoothie through filters to extract each ingredient.
+- _Why?_ Recipes are easier to analyze, compare, and modify than the smoothie itself.
+- _How do we get the smoothie back?_ Blend the ingredients.
**Think With Circles, Not Just Sinusoids**
-The Fourier Transform is about circular paths (not 1-d sinusoids) and Euler's
+The Fourier Transform is about circular paths (not 1-d sinusoids) and Euler's
formula is a clever way to generate one:

Must we use imaginary exponents to move in a circle? Nope. But it's convenient
-and compact. And sure, we can describe our path as coordinated motion in two
-dimensions (real and imaginary), but don't forget the big picture: we're just
+and compact. And sure, we can describe our path as coordinated motion in two
+dimensions (real and imaginary), but don't forget the big picture: we're just
moving in a circle.
**Discovering The Full Transform**
-The big insight: our signal is just a bunch of time spikes! If we merge the
+The big insight: our signal is just a bunch of time spikes! If we merge the
recipes for each time spike, we should get the recipe for the full signal.
The Fourier Transform builds the recipe frequency-by-frequency:
@@ -110,7 +113,7 @@ A few notes:
- k = current frequency we're considering (0 Hertz up to N-1 Hertz)
- Xk = amount of frequency k in the signal (amplitude and phase, a complex number)
- The 1/N factor is usually moved to the reverse transform (going from frequencies back to time). This is allowed, though I prefer 1/N in the forward transform since it gives the actual sizes for the time spikes. You can get wild and even use 1/sqrt(N) on both transforms (going forward and back creates the 1/N factor).
-- n/N is the percent of the time we've gone through. 2 * pi * k is our speed in radians / sec. e^-ix is our backwards-moving circular path. The combination is how far we've moved, for this speed and time.
+- n/N is the percent of the time we've gone through. 2 _ pi _ k is our speed in radians / sec. e^-ix is our backwards-moving circular path. The combination is how far we've moved, for this speed and time.
- The raw equations for the Fourier Transform just say "add the complex numbers". Many programming languages cannot handle complex numbers directly, so you convert everything to rectangular coordinates and add those.
Stuart Riffle has a great interpretation of the Fourier Transform: