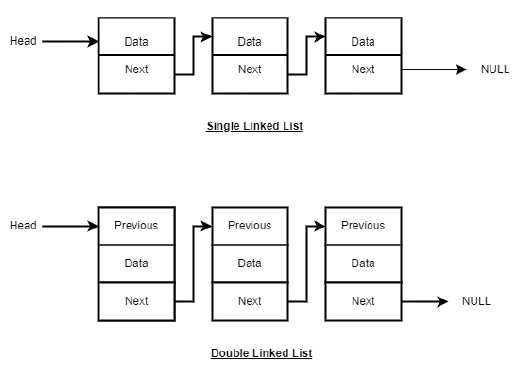
Linked List.md

Linked List

Linked List is a linear data structure that helps us store information at random locations i.e. information is not stored at contiguous memory locations. A linked list is a collection of "nodes". Nodes are blocks which consist of -:

1. Data Field
2. Pointer to the next node

Array allows static allocation of memory which means we need to define the size of array , however we can overcome this problem using Linked List which allows dynamic memory allocation.

Linked List can be seen as chain of nodes where head marks the beginning of the Linked List and tail is used to mark the end of the Linked List. Each node is connected to next node using next pointer.

Types Of Linked List

1. Singly Linked List: The nodes only point to the address of the next node in the list
2. Doubly Linked List: The nodes point to the addresses of both previous and next nodes.
3. Circular Linked List: The last node in the list will point to the first node in the list.

Basic Operations

1. Search

 Node* searchNode(int x){
   Node* temp = head;
   
   while(temp != NULL){
     if(temp->val == x){
         return true;
     }
     temp = temp->next;
   }

   return false;
}

• Time Complexity: O(N), Where N is the number of nodes in the LinkedList
• Auxiliary Space: O(1)

2. Insertion

void addNode(int x){
   Node* ptr = new Node(x);

   if(head == NULL){
     head->next = ptr;
     return;
   }

   Node* temp = head;
   
   while(temp->next != NULL){
     temp = temp->next;
   }
   temp->next = ptr;
   return;
}

• Time complexity: O(N), where N is the number of nodes in the linked list. Since there is a loop from head to end, the function does O(n) work.
• Auxiliary Space: O(1)

3. Deletion

void deleteNode(){
   Node* temp = head;

   while(temp->next != NULL){
     temp = temp->next;
   }

   delete temp;
   return;
}

• Time complexity: O(N), where N is the number of nodes in the linked list. Since there is a loop from head to end, the function does O(n) work.
• Auxiliary Space: O(1)

Popular Algorithms

One of the most popular algorithm in Linked List is Floyd's Cycle-Finding algorithm or Hare and Tortoise Algorithm. Its implemetation can be very well understood using Detect cycle in Linked List.

     Node *detectCycle(Node *head) {
     Node* slow = head;
     Node* fast = head;

     while(fast && fast->next){
         slow = slow->next;
         fast = fast->next->next;

         if(slow == fast){
             fast = head;

             while(fast != slow){
                 fast = fast->next;
                 slow = slow->next;
             }

             return slow;
         }
     }
     return NULL;
     
 }

Solving Least Recently Used (LRU) Cache

class LRUCache {
public:
    class Node{
        public:
        int data;
        int key;
        Node* prev;
        Node* next;

        Node(int data,int key){
            this->data = data;
            this->key = key;
            prev = next = NULL;
        }
    };

    Node* head = new Node(-1,-1);
    Node* tail = new Node(-1,-1);

    unordered_map<int,Node*>m;
    int size = 0;
    LRUCache(int capacity) {
        head->next = tail;
        tail->prev = head;
        size = capacity;
    }
    
    void addNode(Node* ptr){
        Node* temp = head->next;
        head->next = ptr;

        ptr->next = temp;
        ptr->prev = head;
        temp->prev = ptr;
    }

    void deleteNode(Node* node){
        Node* temp = node->prev;
        Node* ptr = node->next;

        temp->next = ptr;
        ptr->prev = temp;
    }

    int get(int key) {
        if(m.find(key) != m.end()){
            Node* node = m[key];
            m.erase(key);

            deleteNode(node);
            addNode(node);
            m[key] = head->next;

            return node->data;
        }
        return -1;
    }
    
    void put(int key, int value) {
        Node* ptr = new Node(value,key);
        
        if(m.find(key) != m.end()){
            Node* temp = m[key];
            deleteNode(temp);
            m.erase(temp->key);
        }

        if(m.size() == size){
            Node* temp = tail->prev;
            deleteNode(temp);
            m.erase(temp->key);
        }
        
        m[key] = ptr;
        addNode(ptr);
    }
};