-
Notifications
You must be signed in to change notification settings - Fork 62
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Simple Infinite Horizon Discrete Time non-stochastic problem #528
Comments
using SDDP
import Ipopt
function main()
δ, ρ = 0.1, 0.05
β = 1 / (1 + ρ)
graph = SDDP.LinearGraph(1)
SDDP.add_edge(graph, 1 => 1, β)
model = SDDP.PolicyGraph(
graph;
sense = :Max,
upper_bound = 1000,
optimizer = Ipopt.Optimizer,
) do sp, _
z = ρ + δ + 0.02
u_SS = (z - ρ - δ) / (ρ + δ)
x_SS = u_SS / δ
x0 = 0.5 * x_SS
@variable(sp, x, SDDP.State, initial_value = x0)
@variable(sp, u)
@constraint(sp, x.out == (1 - δ) * x.in + u)
@stageobjective(sp, z * x.in - u - 0.5 * u^2)
return
end
SDDP.train(model; iteration_limit = 50)
sims = SDDP.simulate(
model,
1,
[:x, :u];
sampling_scheme = SDDP.Historical([(1, nothing) for t in 1:100])
)
return map(sims[1]) do data
return Dict(:u => data[:u], :x => data[:x].out)
end
endyields 100-element Vector{Dict{Symbol, Float64}}:
Dict(:u => 0.13333333331362393, :x => 0.7333333333136239)
Dict(:u => 0.13333333331362374, :x => 0.7933333332958853)
Dict(:u => 0.13333333331362351, :x => 0.8473333332799203)
Dict(:u => 0.13333333331362318, :x => 0.8959333332655515)
Dict(:u => 0.13333333331362332, :x => 0.9396733332526196)
Dict(:u => 0.1333333333136231, :x => 0.9790393332409807)
Dict(:u => 0.13333333331362282, :x => 1.0144687332305053)
Dict(:u => 0.13333333331362288, :x => 1.0463551932210777)
Dict(:u => 0.1333333333136227, :x => 1.0750530072125926)
Dict(:u => 0.13333333331362265, :x => 1.100881039804956)
Dict(:u => 0.13333333331362265, :x => 1.1241262691380831)
Dict(:u => 0.13333333331362265, :x => 1.1450469755378974)
Dict(:u => 0.13333333331362238, :x => 1.16387561129773)
Dict(:u => 0.13333333331362252, :x => 1.1808213834815795)
Dict(:u => 0.13333333331362257, :x => 1.1960725784470443)
Dict(:u => 0.1333333333136224, :x => 1.2097986539159622)
Dict(:u => 0.1333333333136224, :x => 1.2221521218379885)
Dict(:u => 0.13333333331362215, :x => 1.233270242967812)
Dict(:u => 0.13333333331362232, :x => 1.2432765519846531)
Dict(:u => 0.1333333333136223, :x => 1.2522822300998102)
Dict(:u => 0.1333333333136222, :x => 1.2603873404034514)
Dict(:u => 0.13333333331362213, :x => 1.2676819396767285)
Dict(:u => 0.13333333331362227, :x => 1.2742470790226779)
Dict(:u => 0.1333333333136221, :x => 1.2801557044340324)
Dict(:u => 0.13333333331362224, :x => 1.2854734673042514)
Dict(:u => 0.1333333333136221, :x => 1.2902594538874486)
Dict(:u => 0.13333333331362215, :x => 1.294566841812326)
⋮
Dict(:u => 0.13333333331362204, :x => 1.33308667414627)
Dict(:u => 0.13333333331362204, :x => 1.333111340045265)
Dict(:u => 0.13333333331362213, :x => 1.3331335393543606)
Dict(:u => 0.13333333331362204, :x => 1.3331535187325465)
Dict(:u => 0.13333333331362185, :x => 1.3331715001729136)
Dict(:u => 0.13333333331362204, :x => 1.3331876834692442)
Dict(:u => 0.13333333331362188, :x => 1.3332022484359418)
Dict(:u => 0.13333333331362188, :x => 1.3332153569059697)
Dict(:u => 0.13333333331362182, :x => 1.3332271545289944)
Dict(:u => 0.13333333331362174, :x => 1.3332377723897169)
Dict(:u => 0.13333333331362196, :x => 1.333247328464367)
Dict(:u => 0.13333333331362188, :x => 1.3332559289315524)
Dict(:u => 0.13333333331362202, :x => 1.3332636693520192)
Dict(:u => 0.13333333331362207, :x => 1.3332706357304394)
Dict(:u => 0.13333333331362193, :x => 1.3332769054710174)
Dict(:u => 0.13333333331362202, :x => 1.3332825482375377)
Dict(:u => 0.133333333313622, :x => 1.3332876267274059)
Dict(:u => 0.13333333331362204, :x => 1.3332921973682872)
Dict(:u => 0.13333333331362193, :x => 1.3332963109450804)
Dict(:u => 0.13333333331362182, :x => 1.333300013164194)
Dict(:u => 0.13333333331362185, :x => 1.3333033451613967)
Dict(:u => 0.13333333331362188, :x => 1.333306343958879)
Dict(:u => 0.13333333331362182, :x => 1.333309042876613)
Dict(:u => 0.13333333331362193, :x => 1.3333114719025736)
Dict(:u => 0.13333333331362185, :x => 1.3333136580259382)
Dict(:u => 0.13333333331362193, :x => 1.3333156255369663)which looks like the solution from https://discourse.julialang.org/t/solving-the-4-quadrants-of-dynamic-optimization-problems-in-julia-help-wanted/73285/28?u=odow. SDDP.jl is overkill for this sort of problem though. It's not what it was designed for. |
|
Thanks this looks awesome! δ, ρ = 0.1, 0.05; β = 1 / (1 + ρ);
z = ρ + δ + 0.02;
u_SS = (z - ρ - δ) / (ρ + δ);
x_SS = u_SS / δ;
x0 = 0.5 * x_SS;
x0 = 1.5 * x_SS;
opt = Ipopt.Optimizer;
T_sim=300;
#####################################################
graph = SDDP.LinearGraph(1)
SDDP.add_edge(graph, 1 => 1, β)
model = SDDP.PolicyGraph(
graph; sense = :Max, upper_bound = 1000, optimizer = opt,
) do sp, _
@variable(sp, x, SDDP.State, initial_value = x0) # state variable
@variable(sp, u) # control variable
@NLconstraint(sp, x.out == (1-δ)*x.in +(x.in^(0.33)) - u) # transition fcn
@stageobjective(sp, log(u) ) # payoff fcn
# @stageobjective(sp, -(u-0.5)^2 ) # payoff fcn
return
end
ERROR: log is not defined for type AbstractVariableRef. Are you trying to build a nonlinear problem? Make sure you use @NLconstraint/@NLobjective. |
|
We don't support nonlinear objectives just yet. You'll need to add an epigraph variable. model = SDDP.PolicyGraph(
graph; sense = :Max, upper_bound = 1000, optimizer = opt,
) do sp, _
@variable(sp, x, SDDP.State, initial_value = x0) # state variable
@variable(sp, u) # control variable
@NLconstraint(sp, x.out == (1-δ)*x.in +(x.in^(0.33)) - u) # transition fcn
@variable(sp, t)
@NLconstraint(model, t <= log(u))
@stageobjective(sp, t) # payoff fcn
# @stageobjective(sp, -(u-0.5)^2 ) # payoff fcn
return
end |
|
Got an error: ###################################################
δ, ρ = 0.1, 0.05; β = 1 / (1 + ρ);
z = ρ + δ + 0.02;
u_SS = (z - ρ - δ) / (ρ + δ);
x_SS = u_SS / δ;
x0 = 0.5 * x_SS;
x0 = 1.5 * x_SS;
opt = Ipopt.Optimizer;
T_sim=300;
#####################################################
graph = SDDP.LinearGraph(1)
SDDP.add_edge(graph, 1 => 1, β)
model = SDDP.PolicyGraph(
graph; sense = :Max, upper_bound = 1000, optimizer = opt,
) do sp, _
@variable(sp, x, SDDP.State, initial_value = x0) # state variable
@variable(sp, u) # control variable
@NLconstraint(sp, x.out == (1-δ)*x.in +(x.in^(0.33)) - u) # transition fcn
@variable(sp, t)
@NLconstraint(model, t <= log(u))
@stageobjective(sp, t) # payoff fcn
# @stageobjective(sp, -(u-0.5)^2 ) # payoff fcn
return
end
ERROR: Expected model to be a JuMP model, but it has type SDDP.PolicyGraph{Int64} |
|
Oh. |
|
I wish I understood your pkg well enough to troubleshoot on my own ###################################################
δ, ρ = 0.1, 0.05; β = 1 / (1 + ρ);
z = ρ + δ + 0.02;
u_SS = (z - ρ - δ) / (ρ + δ);
x_SS = u_SS / δ;
x0 = 0.5 * x_SS;
x0 = 1.5 * x_SS;
opt = Ipopt.Optimizer;
T_sim=300;
#####################################################
graph = SDDP.LinearGraph(1)
SDDP.add_edge(graph, 1 => 1, β)
model = SDDP.PolicyGraph(
graph; sense = :Max, upper_bound = 1000, optimizer = opt,
) do sp, _
@variable(sp, x, SDDP.State, initial_value = x0) # state variable
@variable(sp, u) # control variable
@NLconstraint(sp, x.out == (1-δ)*x.in +(x.in^(0.33)) - u) # transition fcn
@variable(sp, t)
@NLconstraint(sp, t <= log(u))
@stageobjective(sp, t) # payoff fcn
# @stageobjective(sp, -(u-0.5)^2 ) # payoff fcn
return
end
A policy graph with 1 nodes.
Node indices: 1
------------------------------------------------------------------------------
SDDP.jl (c) Oscar Dowson, 2017-21
Problem
Nodes : 1
State variables : 1
Scenarios : Inf
Existing cuts : false
Subproblem structure : (min, max)
Variables : (5, 5)
VariableRef in MOI.LessThan{Float64} : (1, 1)
Options
Solver : serial mode
Risk measure : SDDP.Expectation()
Sampling scheme : SDDP.InSampleMonteCarlo
Numerical stability report
Non-zero Matrix range [0e+00, 0e+00]
Non-zero Objective range [1e+00, 1e+00]
Non-zero Bounds range [1e+03, 1e+03]
Non-zero RHS range [0e+00, 0e+00]
No problems detected
Iteration Simulation Bound Time (s) Proc. ID # Solves
┌ Warning: Attempting to recover from serious numerical issues...
└ @ SDDP ~/.julia/packages/SDDP/VpZOu/src/algorithm.jl:261
ERROR: Unable to retrieve solution from 1.
Termination status: INVALID_MODEL
Primal status: UNKNOWN_RESULT_STATUS
Dual status: UNKNOWN_RESULT_STATUS.
A MathOptFormat file was written to `subproblem_1.mof.json`.
See https://odow.github.io/SDDP.jl/latest/tutorial/06_warnings/#Numerical-stability-1
for more information.
Stacktrace:
[1] error(::String, ::String, ::String, ::String, ::String, ::String, ::String)
@ Base ./error.jl:44
[2] write_subproblem_to_file(node::SDDP.Node{Int64}, filename::String; throw_error::Bool)
@ SDDP ~/.julia/packages/SDDP/VpZOu/src/algorithm.jl:236
[3] attempt_numerical_recovery(node::SDDP.Node{Int64})
@ SDDP ~/.julia/packages/SDDP/VpZOu/src/algorithm.jl:272
[4] solve_subproblem(model::SDDP.PolicyGraph{Int64}, node::SDDP.Node{Int64}, state::Dict{Symbol, Float64}, noise::Nothing, scenario_path::Vector{Tuple{Int64, Any}}; duality_handler::Nothing)
@ SDDP ~/.julia/packages/SDDP/VpZOu/src/algorithm.jl:393
[5] macro expansion
@ ~/.julia/packages/SDDP/VpZOu/src/plugins/forward_passes.jl:84 [inlined]
[6] macro expansion
@ ~/.julia/packages/TimerOutputs/4yHI4/src/TimerOutput.jl:237 [inlined]
[7] forward_pass(model::SDDP.PolicyGraph{Int64}, options::SDDP.Options{Int64}, #unused#::SDDP.DefaultForwardPass)
@ SDDP ~/.julia/packages/SDDP/VpZOu/src/plugins/forward_passes.jl:83
[8] macro expansion
@ ~/.julia/packages/SDDP/VpZOu/src/algorithm.jl:782 [inlined]
[9] macro expansion
@ ~/.julia/packages/TimerOutputs/4yHI4/src/TimerOutput.jl:237 [inlined]
[10] iteration(model::SDDP.PolicyGraph{Int64}, options::SDDP.Options{Int64})
@ SDDP ~/.julia/packages/SDDP/VpZOu/src/algorithm.jl:781
[11] master_loop
@ ~/.julia/packages/SDDP/VpZOu/src/plugins/parallel_schemes.jl:32 [inlined]
[12] train(model::SDDP.PolicyGraph{Int64}; iteration_limit::Int64, time_limit::Nothing, print_level::Int64, log_file::String, log_frequency::Int64, run_numerical_stability_report::Bool, stopping_rules::Vector{SDDP.AbstractStoppingRule}, risk_measure::SDDP.Expectation, sampling_scheme::SDDP.InSampleMonteCarlo, cut_type::SDDP.CutType, cycle_discretization_delta::Float64, refine_at_similar_nodes::Bool, cut_deletion_minimum::Int64, backward_sampling_scheme::SDDP.CompleteSampler, dashboard::Bool, parallel_scheme::SDDP.Serial, forward_pass::SDDP.DefaultForwardPass, forward_pass_resampling_probability::Nothing, add_to_existing_cuts::Bool, duality_handler::SDDP.ContinuousConicDuality, forward_pass_callback::SDDP.var"#73#77")
@ SDDP ~/.julia/packages/SDDP/VpZOu/src/algorithm.jl:1041
[13] top-level scope
@ ~/Dropbox/Computation/Julia/4prob_new/3_Invest_CapStruct_Default/2a_Firm_Invest/Invest/SDDP.jl:99
julia> |
|
I should have thought about this a fraction more. The issue now is that |
|
Got it to work using SDDP, Plots
import Ipopt
α=.33; δ=1.0; z=1.0; β=.98;
s_ss = (((1/β) -1 +δ)/(α*z))^(1/(α-1))
c_ss = z*(s_ss)^(α) - δ*s_ss
opt = Ipopt.Optimizer;
T_sim=100;
#####################################################
graph = SDDP.LinearGraph(1)
SDDP.add_edge(graph, 1 => 1, β)
model = SDDP.PolicyGraph(
graph; sense = :Max, upper_bound = 1000, optimizer = opt,
) do sp, _
@variable(sp, x >= 1e-5, SDDP.State, initial_value = 1.0) # state variable
@variable(sp, u >= 1e-5) # control variable
@NLconstraint(sp, x.out == (1-δ)*x.in +(x.in^α) - u) # transition fcn
@variable(sp, t)
@NLconstraint(sp, t <= log(u + 1e-9))
@stageobjective(sp, t) # payoff fcn
# @stageobjective(sp, -(u-0.5)^2 ) # payoff fcn
return
end
SDDP.train(model; iteration_limit = 100)
sims = SDDP.simulate(model, 1, [:x, :u];
sampling_scheme = SDDP.Historical([(1, nothing) for t in 1:T_sim])
);
sim_K = map(data -> data[:x].out, sims[1])
sim_i = map(data -> data[:u], sims[1])
plot(legend=:topright) #, ylims = (0,2)
plot!(sim_K, c=1, lab="K")
plot!(1:T_sim, tt -> s_ss, c=1, l=:dash, lw=3, lab = "K_SS")
plot!(sim_i, c=2, lab="c")
plot!(1:T_sim, tt -> c_ss, c=2, l=:dash, lw=3, lab = "i_SS")
|
Three parts to this:
So this is probably never going to compete with discretization methods for the trivial, but nonlinear, problem classes that you're exploring.
You can break a lot of the assumptions and things still work. The problem is, we loose convergence guarantees on the solution that you'll end up with. If things stay convex, you're safe. If the problem is non-convex, then you'll run into trouble.
It depends. <100? The answer really depends though. For deterministic problems, maybe more. For stochastic problems, sometimes even 3 or 4 states becomes really hard to solve. As an indication, the NZ electricity system model has O(10^1) states, O(10^2) control variables and constraints, 52 stages with one cycle, and stagewise independent uncertainty, and it takes 24 hours to solve.
sims = SDDP.simulate(model, 1, [:x, :u];
sampling_scheme = SDDP.Historical([(1, nothing) for t in 1:T_sim]),
incoming_state = Dict("x" => 10.0),
);Untested, but try something like: rule = SDDP.DecisionRule(model, 1)
SDDP.evaluate(
rule;
incoming_state = Dict(:x => 10.0),
conntrols_to_record = [:u],
)https://odow.github.io/SDDP.jl/stable/apireference/#SDDP.DecisionRule I notice there's actually an API uniformity issue; one is the |
|
When economists solve Stochastic DP problems, usually they can handle up to 5 state variables. |
|
But just for a ballpark figure, if there are 1000 state variables, and each state has two potential values (on/off), then there are 2^1000 (~10^300) values in the state-space, and normal dynamic programming would need to evaluate each of those. So it's impossible to solve those problems exactly. You need some sort of approximation or clever algorithm. In a way, SDDP.jl is just doing value function iteration using linear programs instead of a discretization scheme. So not only does it have the downsides of value function iteration, but it also requires solving a linear program at each step instead of directly evaluating the cost function. |
|
Thanks for the interesting discussion. I have some plans for revamped documentation, #496, which will include some examples from finance. Closing because this isn't a bug and other issues cover the documentation feature request. |

Hi, can you please help me solve the following problem with SDDP.jl using
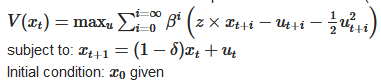
Ipoptor another open-source solver:I use the following parameters:
I spent some time trying and was not able to get it to work...
The text was updated successfully, but these errors were encountered: