diff --git a/README.md b/README.md
index 3f9f0b07..9287ee92 100755
--- a/README.md
+++ b/README.md
@@ -5,6 +5,7 @@ I am trying a new initiative - a-paper-a-week. This repository will hold all tho
## List of papers
+* [Hamiltonian Neural Networks](https://shagunsodhani.com/papers-I-read/Hamiltonian-Neural-Networks)
* [Extrapolating Beyond Suboptimal Demonstrations via Inverse Reinforcement Learning from Observations](https://shagunsodhani.com/papers-I-read/Extrapolating-Beyond-Suboptimal-Demonstrations-via-Inverse-Reinforcement-Learning-from-Observations)
* [Meta-Reinforcement Learning of Structured Exploration Strategies](https://shagunsodhani.com/papers-I-read/Meta-Reinforcement-Learning-of-Structured-Exploration-Strategies)
* [Good-Enough Compositional Data Augmentation](https://shagunsodhani.com/papers-I-read/Good-Enough-Compositional-Data-Augmentation)
diff --git a/site/_posts/2019-06-20-Hamiltonian Neural Networks.md b/site/_posts/2019-06-20-Hamiltonian Neural Networks.md
new file mode 100755
index 00000000..9c326c2c
--- /dev/null
+++ b/site/_posts/2019-06-20-Hamiltonian Neural Networks.md
@@ -0,0 +1,56 @@
+---
+layout: post
+title: Hamiltonian Neural Networks
+comments: True
+excerpt:
+tags: ['2019', AI, Physics]
+
+---
+
+## Introduction
+
+* The paper proposes a very cool idea at the intersection of deep learning and physics.
+
+* The idea is to train a neural network architecture that builds on the concept of Hamiltonian Mechanics (from Physics) to learn physical conservation laws in an unsupervised manner.
+
+* [Link to the paper](https://arxiv.org/abs/1906.01563)
+
+* [Link to the code](https://github.com/greydanus/hamiltonian-nn)
+
+* [Link to author's blog](https://greydanus.github.io/2019/05/15/hamiltonian-nns/)
+
+## Hamiltonian Mechanics
+
+* It is a branch of physics that can describe systems which follow some conservation laws and invariants.
+
+* Consider a set of *N* pair of coordinates [(q1, p1), ..., (qN, pN)] where **q** = [q1, ..., qN] dnotes the position of the set of objects while **p** = [p1, ..., pN] denotes the momentum of the set of variables.
+
+* Together these *N* pairs completely describe the system.
+
+* A scalar function *H(**q**, **p**)*, called as the Hamiltonian is defined such that the partial derivative of *H* with respect to **p** is equal to derivative of **q** with respect to time *t* and the negative of partial derivative of *H* with respect to **q** is equal to derivative of **p** with respect to time *t*.
+
+* This can be expressed in the form of the equation as follows:
+
+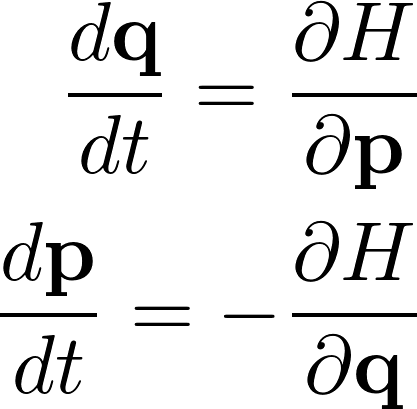 +
+* The Hamiltonian can be tied to the total energy of the system and can be used in any system where the total energy is conserved.
+
+## Hamiltonian Neural Network (HNN)
+
+* The Hamiltonian *H* can be parameterized using a neural network and can learn conserved quantities from the data in an unsupervised manner.
+
+* The loss function looks as follows:
+
+
+
+* The Hamiltonian can be tied to the total energy of the system and can be used in any system where the total energy is conserved.
+
+## Hamiltonian Neural Network (HNN)
+
+* The Hamiltonian *H* can be parameterized using a neural network and can learn conserved quantities from the data in an unsupervised manner.
+
+* The loss function looks as follows:
+
+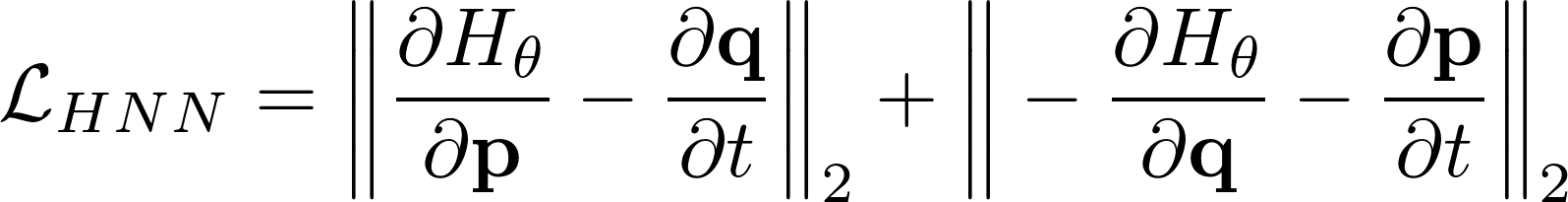 +
+* The partial derivatives can be obtained by computing the *in-graph* gradient of the output variables with respect to the input variables.
+
+## Observations
+
+* For setups where the energy must be conserved exactly, (eg ideal mass-spring and ideal pendulum), the HNN learn to preserve an energy-like scalar.
+
+* For setups where the energy need not be conserved exactly, the HNNs still learn to preserve the energy thus highlighting a limitation of HNNs.
+
+* In case of two body problems, the HNN model is shown to be much more robust when making predictions over longer time horizons as compared to the baselines.
+
+* In the final experiment, the model is trained on pixel observations and not state observations. In this case, two auxiliary losses are added: auto-encoder reconstruction loss and a loss on the latent space representations. Similar to the previous experiments, the HNN model makes robust predictions over much longer time horizons.
\ No newline at end of file
+
+* The partial derivatives can be obtained by computing the *in-graph* gradient of the output variables with respect to the input variables.
+
+## Observations
+
+* For setups where the energy must be conserved exactly, (eg ideal mass-spring and ideal pendulum), the HNN learn to preserve an energy-like scalar.
+
+* For setups where the energy need not be conserved exactly, the HNNs still learn to preserve the energy thus highlighting a limitation of HNNs.
+
+* In case of two body problems, the HNN model is shown to be much more robust when making predictions over longer time horizons as compared to the baselines.
+
+* In the final experiment, the model is trained on pixel observations and not state observations. In this case, two auxiliary losses are added: auto-encoder reconstruction loss and a loss on the latent space representations. Similar to the previous experiments, the HNN model makes robust predictions over much longer time horizons.
\ No newline at end of file
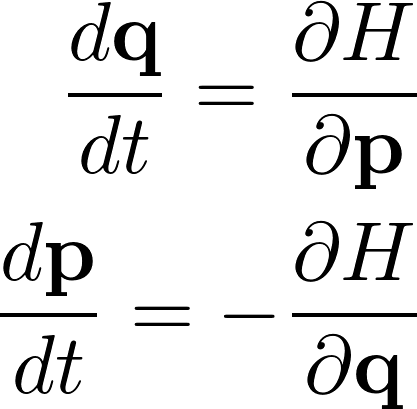 +
+* The Hamiltonian can be tied to the total energy of the system and can be used in any system where the total energy is conserved.
+
+## Hamiltonian Neural Network (HNN)
+
+* The Hamiltonian *H* can be parameterized using a neural network and can learn conserved quantities from the data in an unsupervised manner.
+
+* The loss function looks as follows:
+
+
+
+* The Hamiltonian can be tied to the total energy of the system and can be used in any system where the total energy is conserved.
+
+## Hamiltonian Neural Network (HNN)
+
+* The Hamiltonian *H* can be parameterized using a neural network and can learn conserved quantities from the data in an unsupervised manner.
+
+* The loss function looks as follows:
+
+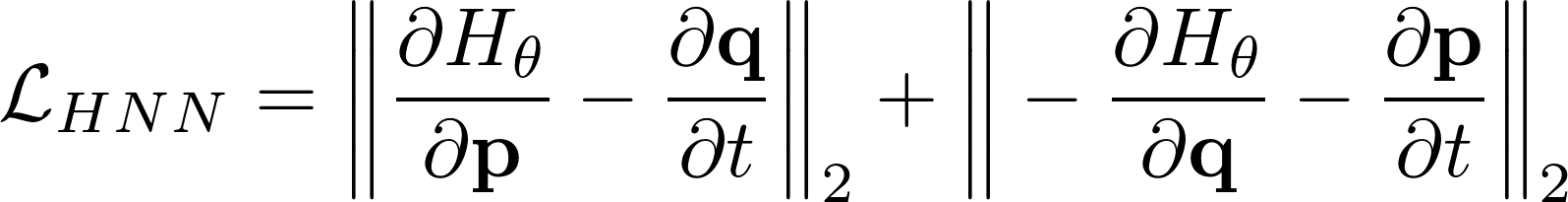 +
+* The partial derivatives can be obtained by computing the *in-graph* gradient of the output variables with respect to the input variables.
+
+## Observations
+
+* For setups where the energy must be conserved exactly, (eg ideal mass-spring and ideal pendulum), the HNN learn to preserve an energy-like scalar.
+
+* For setups where the energy need not be conserved exactly, the HNNs still learn to preserve the energy thus highlighting a limitation of HNNs.
+
+* In case of two body problems, the HNN model is shown to be much more robust when making predictions over longer time horizons as compared to the baselines.
+
+* In the final experiment, the model is trained on pixel observations and not state observations. In this case, two auxiliary losses are added: auto-encoder reconstruction loss and a loss on the latent space representations. Similar to the previous experiments, the HNN model makes robust predictions over much longer time horizons.
\ No newline at end of file
+
+* The partial derivatives can be obtained by computing the *in-graph* gradient of the output variables with respect to the input variables.
+
+## Observations
+
+* For setups where the energy must be conserved exactly, (eg ideal mass-spring and ideal pendulum), the HNN learn to preserve an energy-like scalar.
+
+* For setups where the energy need not be conserved exactly, the HNNs still learn to preserve the energy thus highlighting a limitation of HNNs.
+
+* In case of two body problems, the HNN model is shown to be much more robust when making predictions over longer time horizons as compared to the baselines.
+
+* In the final experiment, the model is trained on pixel observations and not state observations. In this case, two auxiliary losses are added: auto-encoder reconstruction loss and a loss on the latent space representations. Similar to the previous experiments, the HNN model makes robust predictions over much longer time horizons.
\ No newline at end of file