【Python】实现二维装箱Bottom-Left算法及可视化

1 题目

将若干个矩形物品装进矩形箱子中，并且在装箱的过程中不允许将矩形物品斜着放，即平行于横坐标。一般来说求解的目标是最小化箱子的箱子数目或者是箱子空间占用率。

当该算法适用于矩阵存储时，求解的最优目标是箱子的最大化空间占用率。以下即是求解的过程

2 装箱算法

2.1 所有装箱算法

参考【A Thousand Ways to Pack the Bin - A Practical Approach to Two-Dimensional Rectangle Bin Packing】

以下我将会介绍其中一种叫Bottom-Left装箱算法。算法过程就是，矩形从箱子的右上角开始进入，先尽可能向下移动，再向左移动，一直循环，直至不再移动。在以下算法过程中，以0-1背包问题的思路去实现，即某个矩形装进箱子，则flag相应为1，未装进的flag为0。输出单个箱子占用率。

2.2 Bottom-Left具体算法过程

初始化是，输入箱子大小[W,H]

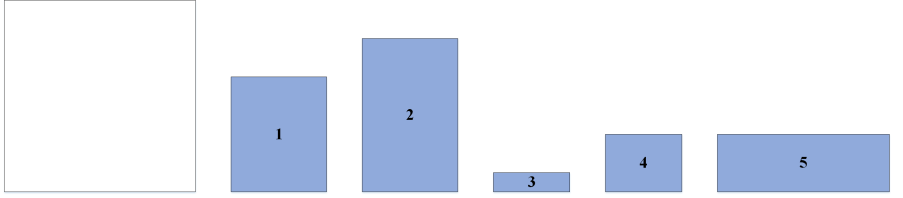
再输入每一个矩形的长和宽

4 5

4 7

4 2

4 4

7 4

初始装箱顺序为：12345

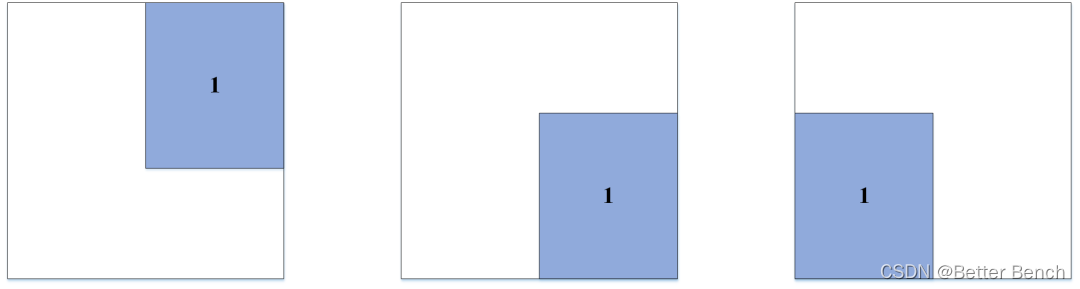
第一步：装第一个矩形，从右上角进入，一直向下移动，然后移动一直向左移动，直到左下角。用一个列表记录装进箱子的矩阵。表示为【x,y,width,height】x和y使右上角坐标。该矩形的flag标记为1。

第二步：装第二个矩形，先将矩形放入右上角，再判断第二个矩形是否与箱子中的矩形是否相交（overlap函数）。如果相交，就不放进箱子，换下一个矩形，如果不相交，计算可向下移动的距离（downHAtPoint函数），向下移动，并更新矩形位置（Update_itemRP函数），最后计算可向左移动的距离（leftWAtPoint函数），向左移动，并更新位置，直至可移动距离为0。将第二个矩形最终位置信息【x,y,width,height】添加进列表。该矩形的flag标记未1。

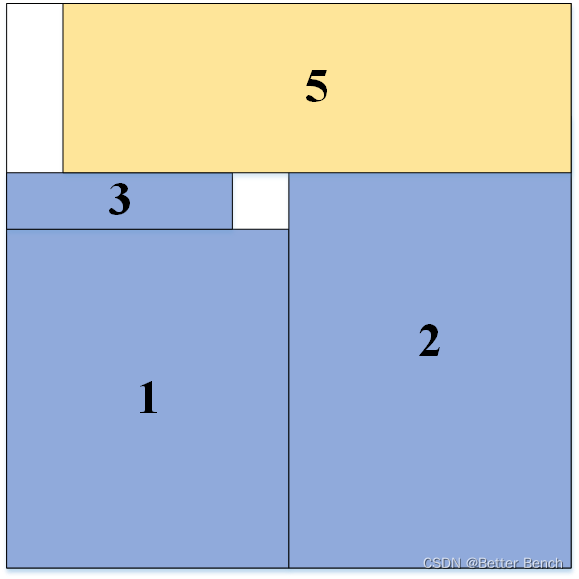
第三步：剩下的矩形，和第二步一样。如果该矩形装不进箱子，就换下一个矩阵，继续装，直至遍历完所有箱子。

3 Python 实现

本算法实现中，只用了一个箱子。如果想要多个箱子来装，可以修改本人去掉注释的地方，启用下一个箱子。

3.1 main.py主函数

from tools import *
import random

#   BL（bottom-up left-justified）法求解二位装箱问题
#   @BetterBench
#   思想：首先将选中的物体放在箱子的右上角，然后尽量向下向左作连续移动，直到不能移动为止
# 输入参数
itemNum=30 #物品数目
AllItem=np.array([[random.randint(1, 5) for j in range(1, 3)] for i in range(1,itemNum+1)])  #随机生成30个物品，[width,height]
Bin=[10,10] #箱子宽度与高度
ran=list(range(itemNum))
random.shuffle(ran) #随机生成装箱序列

ansBXY=np.zeros((itemNum,3))  #[箱子编号，X坐标，Y坐标]
RPNXY=[];
BinNum=1;
flagItem=np.zeros(itemNum) #标记物品是否被装入箱子，0没有装入，1装入
# 开始装箱

for i in range(itemNum):
    if flagItem[ran[i]]==0:
        item=AllItem[ran[i],:]
        itemRP=Bin  #起点全部在箱子右上角顶点
        flagOL=overlap(item,AllItem,itemRP,RPNXY) #如果重合flagOL=1；反之flagOL=0
        if flagOL==0:
            itemRP=finalPos(item,AllItem,itemRP,RPNXY) #更新物品从当前位置向下向左移动后到最终位置后右上角顶点坐标
            RPNXY.append([ran[i],itemRP[0],itemRP[1]]) # 记录装进箱子的矩形【ID,width,height】
            flagItem[ran[i]]=1
# 启用第下一个箱子
# if list(flagItem).count(0)>0:
#     BinNum=BinNum+1
#     RPNXY=[]

输出哪些矩形被装进箱子

print(flagItem)

array([0., 0., 1., 1., 1., 0., 1., 0., 1., 1., 0., 0., 1., 1., 1., 1., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0.])

计算箱子占用率

rect_area = 0
bin_area = Bin[0]*Bin[1]
for id in RPNXY:
  width,height = AllItem[id[0]]
  rect_area += width*height
print('占用率:{}'.format(rect_area/bin_area))

占用率:0.81

可视化装箱后的结果

import matplotlib.pyplot as plt
import matplotlib.patches as patches
import random
fig, ax = plt.subplots(1, 1)
ax1 = fig.gca()
for i in RPNXY:
    width,height = AllItem[i[0]]
    rx,ry = i[1],i[2]
    lx,ly = rx-width,ry-height
    plt.xlim((0, Bin[0]))
    plt.ylim((0, Bin[1]))
    color = "#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])
    rect = patches.Rectangle((lx, ly), width,height,linewidth=1, facecolor = color)
    ax1.add_patch(rect)
plt.show()