-
Notifications
You must be signed in to change notification settings - Fork 190
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
[Proposal] Rotation and Anisotropy in N-D #138
Comments
|
It is indeed a valid point that I haven't considered before. I'm not competent on this subject, so I can't really give you useful input on this proposal.
As a side note, we don't necessarily have to resolve this for N-D krigging refactoring. Having one interface for 1D, 2D, 3D would already be great and address most common use cases. In a first approach one could say that N > 3 are not supported, and then in a second phase add support for it if there is interest. |
|
With the above formulation, it should be quite easy to implement. So we can get rid of different classes for different dimensions. PS: I updated the issue to fix some wrong calculations. |
|
This looks good to me, and shouldn't be too hard to implement for arbitrary dimensions. At one point, @rth had suggested refactoring the rotation/scaling into a general 'anisotropy transformation' that could be implemented as part of a pipeline, similar to how things are done in scikit-learn. Maybe worth separating the anisotropy stuff out from the whole kriging code (currently the anisotropy adjustments are pretty well baked into the main PyKrige code), would at the very least make code maintenance somewhat easier. |
|
I am planing to include the transformation matrices in the covariance model in |
|
I really like the idea. I've started a GSTools PR to get things started. |
|
In order to be in line with the Tait-Bryan angles, the signs of the |
|
This is now solved in GSTools and will be used in PyKrige in the future: |
In order to provide N-D kriging, we should think about, what rotation and anisotropy means in higher dimensions.
My proposal is:
Rotation
in N-D we can describe rotation with M angles:
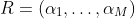

where M is the number of 2D sub-spaces (from main axis):
each angle describes the rotation in the x_i-x_j sub-space where the indices are given in the following order:

the rotation-matrix for a given angle in the i-j plane is given by:
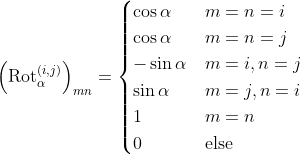
consequently, the rotation matrix to bring unrotated coordinates into the desired rotation is given by:

since we are interested in derotating given points, we calculate the derotation matrix with:

Anisotropy
Anisotropy is given by N-1 anisotropy factors

We can also formulate a transformation matrix by:
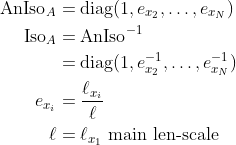
normalized lag
The normalized lag (Isotropified and derotated) is now given by:
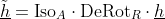
Conclusion
The proposed formulation coincides with the current descriptions of rotation and anisotropy in 1D (none), 2D (rotation in x-y plane, 1 aniso-factor) and 3D (Tait–Bryan angles, 2 aniso-factors) and generalizes them to N-D.
What do you think? @rth, @bsmurphy, @LSchueler
The text was updated successfully, but these errors were encountered: