Update Fourier README.

src/algorithms/math/fast-fourier-transform/README.md

@@ -1,11 +1,89 @@
-# Discrete Fourier transform
-The Discrete Fourier transform transforms a sequence of `N` complex numbers  
-**{x<sub>n</sub>}** := **x<sub>0</sub>, x<sub>1</sub>, x<sub>2</sub> ..., x<sub>N-1</sub>**  &nbsp;&nbsp;into another sequence of complex numbers <br> **{X<sub>k</sub>}** := **X<sub>0</sub>, X<sub>1</sub>, X<sub>2</sub> ..., X<sub>N-1</sub>**&nbsp;&nbsp;&nbsp; which is defined by
+# Fourier Transform
 
-![alt text](https://wikimedia.org/api/rest_v1/media/math/render/svg/1af0a78dc50bbf118ab6bd4c4dcc3c4ff8502223)
+## Definitions
 
+The **Fourier Transform** (**FT**) decomposes a function of time (a signal) into 
+the frequencies that make it up, in a way similar to how a musical chord can be 
+expressed as the frequencies (or pitches) of its constituent notes.
+
+The **Discrete Fourier Transform** (**DFT**) converts a finite sequence of 
+equally-spaced samples of a function into a same-length sequence of 
+equally-spaced samples of the discrete-time Fourier transform (DTFT), which is a 
+complex-valued function of frequency. The interval at which the DTFT is sampled 
+is the reciprocal of the duration of the input sequence. An inverse DFT is a 
+Fourier series, using the DTFT samples as coefficients of complex sinusoids at 
+the corresponding DTFT frequencies. It has the same sample-values as the original 
+input sequence. The DFT is therefore said to be a frequency domain representation 
+of the original input sequence. If the original sequence spans all the non-zero 
+values of a function, its DTFT is continuous (and periodic), and the DFT provides 
+discrete samples of one cycle. If the original sequence is one cycle of a periodic 
+function, the DFT provides all the non-zero values of one DTFT cycle.
+
+The Discrete Fourier transform transforms a sequence of `N` complex numbers:
+
+{x<sub>n</sub>} = x<sub>0</sub>, x<sub>1</sub>, x<sub>2</sub> ..., x<sub>N-1</sub>
+
+into another sequence of complex numbers:
+
+{X<sub>k</sub>} = X<sub>0</sub>, X<sub>1</sub>, X<sub>2</sub> ..., X<sub>N-1</sub>
+
+which is defined by:
+
+![DFT](https://wikimedia.org/api/rest_v1/media/math/render/svg/1af0a78dc50bbf118ab6bd4c4dcc3c4ff8502223)
+
+The **Discrete-Time Fourier Transform** (**DTFT**) is a form of Fourier analysis 
+that is applicable to the uniformly-spaced samples of a continuous function. The 
+term discrete-time refers to the fact that the transform operates on discrete data
+(samples) whose interval often has units of time. From only the samples, it 
+produces a function of frequency that is a periodic summation of the continuous 
+Fourier transform of the original continuous function.
+
+A **Fast Fourier Transform** (**FFT**) is an algorithm that samples a signal over
+a period of time (or space) and divides it into its frequency components. These 
+components are single sinusoidal oscillations at distinct frequencies each with 
+their own amplitude and phase.
+
+This transformation is illustrated in Diagram below. Over the time period measured
+in the diagram, the signal contains 3 distinct dominant frequencies.
+
+View of a signal in the time and frequency domain:
+
+![FFT](https://upload.wikimedia.org/wikipedia/commons/6/61/FFT-Time-Frequency-View.png)
+
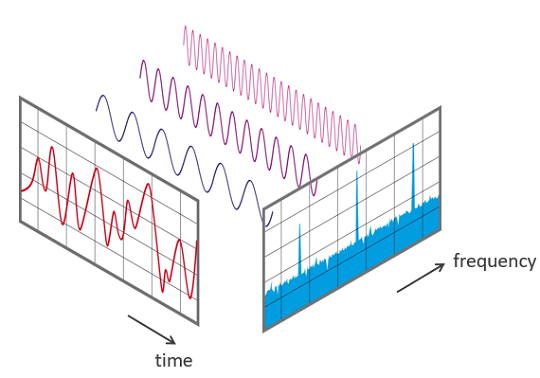+An FFT algorithm computes the discrete Fourier transform (DFT) of a sequence, or 
+its inverse (IFFT). Fourier analysis converts a signal from its original domain 
+to a representation in the frequency domain and vice versa. An FFT rapidly 
+computes such transformations by factorizing the DFT matrix into a product of 
+sparse (mostly zero) factors. As a result, it manages to reduce the complexity of 
+computing the DFT from O(n<sup>2</sup>), which arises if one simply applies the 
+definition of DFT, to O(n log n), where n is the data size.
+
+Here a discrete Fourier analysis of a sum of cosine waves at 10, 20, 30, 40, 
+and 50 Hz:
+
+![FFT](https://upload.wikimedia.org/wikipedia/commons/6/64/FFT_of_Cosine_Summation_Function.png)
+
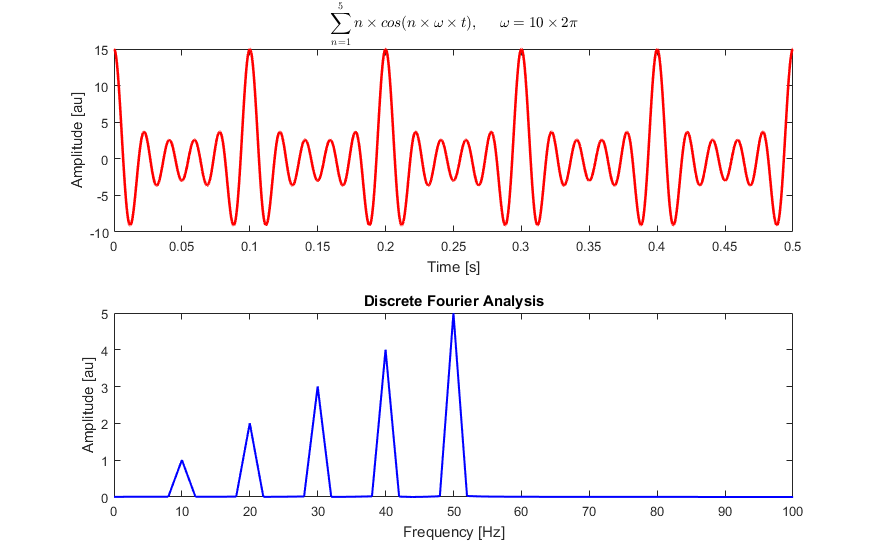+## Explanation
+
+The Fourier Transform is one of deepest insights ever made. Unfortunately, the 
+meaning is buried within dense equations:
+
+![](https://betterexplained.com/wp-content/plugins/wp-latexrender/pictures/45c088dbb767150fc0bacfeb49dd49e5.png)
+![](https://betterexplained.com/wp-content/plugins/wp-latexrender/pictures/faeb9c5bf2e60add63ae4a70b293c7b4.png)
+
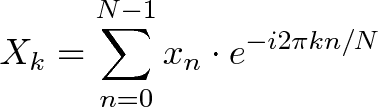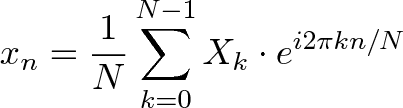+Rather than jumping into the symbols, let's experience the key idea firsthand. Here's a plain-English metaphor:
+
+- *What does the Fourier Transform do?* Given a smoothie, it finds the recipe.
+- *How?* Run the smoothie through filters to extract each ingredient.
+- *Why?* Recipes are easier to analyze, compare, and modify than the smoothie itself.
+- *How do we get the smoothie back?* Blend the ingredients.
 
 ## References
 
+- [An Interactive Guide To The Fourier Transform](https://betterexplained.com/articles/an-interactive-guide-to-the-fourier-transform/)
+- [YouTube by Better Explained](https://www.youtube.com/watch?v=iN0VG9N2q0U&t=0s&index=77&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
+- [YouTube by 3Blue1Brown](https://www.youtube.com/watch?v=spUNpyF58BY&t=0s&index=76&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
+- [Wikipedia, FT](https://en.wikipedia.org/wiki/Fourier_transform)
 - [Wikipedia, DFT](https://www.wikiwand.com/en/Discrete_Fourier_transform)
+- [Wikipedia, DTFT](https://en.wikipedia.org/wiki/Discrete-time_Fourier_transform)
 - [Wikipedia, FFT](https://www.wikiwand.com/en/Fast_Fourier_transform)