- Introduction
- Installation
- How-Tos
- Implemented Algorithms, Search Spaces, and Problems
- Data Formats
- Evaluating Experiments
- Examples
- More Features
- Uselful Links and References
- Publications on moptipy and Works using moptipy
- License
- Contact
moptipy is a library with implementations of metaheuristic optimization methods in Python 3.12 that also offers an environment for replicable experiments.
The framework, algorithm implementations, and the library design are accompanied by the book Optimization Algorithms.
The library is structured with performance, ease-of-use, and generality in mind, but also based on an educational and research perspective.
It is therefore (hopefully) suitable for practical industrial applications, scientific research, and for students who are just entering the field of metaheuristic optimization.
Metaheuristic optimization algorithms are methods for solving hard problems.
moptipy provides an API, several algorithm implementations, as well as experiment execution and evaluation facilities for metaheuristics.
A metaheuristic algorithm can be a black-box method, which can solve problems without deeper knowledge about their nature.
Such a black-box algorithm only requires methods to create and modify points in the search space and to evaluate their quality.
With these operations, it will try to discover better solutions step-by-step.
Black-box metaheuristics are very general and can be adapted to almost any optimization problem.
They allow us to plug in almost arbitrary search operators, search spaces, and objective functions.
But it is also possible to develop algorithms that are tailored to specified problems.
For example, one could either design the search operators and the optimization algorithm as a unit.
Then, the algorithm could change its way to sample new points based on the information it gathers.
Or one could design an algorithm for a specific search space, say, the n-dimensional real numbers, which could then make use of the special features of this space, such as arithmetic and geometric relationships of the points within it.
Or one could design an algorithm for a specific problem, making use of specific features of the objective function.
Finally, there are multi-objective optimization problems where multiple, potentially conflicting, criteria need to be optimized at once.
Within our moptipy framework, you can implement algorithms of all of these types under a unified API.
Our package already provides a growing set of algorithms and adaptations to different search spaces as well as a set of well-known optimization problems.
What moptipy also offers is an experiment execution facility that can collect detailed log information and evaluate the gathered results in a reproducible fashion.
The moptipy API supports both single-objective and multi-objective optimization.
A set of "How-Tos" is given in Section 3 and a longer list of examples is given in Section 7.
You can also take a look at our moptipy flyer.
Examples and practical applications of moptipy can be found in the moptipyapps package, which is available on GitHub and in PyPi.
In order to use this package and to, e.g., run the example codes, you need to first install it using pip or some other tool that can install packages from PyPi.
You can install the newest version of this library from PyPi using pip by doing
pip install moptipyThis will install the latest official release of our package as well as all dependencies. If you want to install the latest source code version from GitHub (which may not yet be officially released), you can do
pip install git+https://github.com/thomasWeise/moptipy.gitIf you want to install the latest source code version from GitHub (which may not yet be officially released) and you have set up a private/public key for GitHub, you can also do:
git clone ssh://[email protected]/thomasWeise/moptipy
pip install moptipyThis may sometimes work better if you are having trouble reaching GitHub via https or http.
You can also clone the repository and then run a make build, which will automatically install all dependencies, run all the tests, and then install the package on your system, too.
This will work only on Linux, though.
It also installs the dependencies for building, which include, e.g., those for unit testing and static analysis.
If this build completes successful, you can be sure that moptipy will work properly on your machine.
All dependencies for using and running moptipy are listed at here.
The additional dependencies for a full make build, including unit tests, static analysis, and the generation of documentation are listed here.
You can find many examples of how to use the moptipy library in the folder "examples".
Here, we talk mainly about directly applying one or multiple optimization algorithm(s) to one or multiple optimization problem instance(s).
In Section 5 on Data Formats, we give examples and specifications of the log files that our system produces and how you can export the data to other formats.
Later, in Section 6 on Evaluating Experiments, we provide several examples on how to evaluate and visualize the results of experiments.
In Section 7 on examples, we list all the examples that ship with moptipy.
The most basic task that we can do in the domain of optimization is to apply one algorithm to one instance of an optimization problem.
In our framework, we refer to this as an "execution."
You can prepare an execution using the class Execution in the module moptipy.api.execution.
This class follows the builder design pattern.
A builder is basically an object that allows you to step-by-step set the parameters of another, more complicated object that should be created.
Once you have set all parameters, you can create the object.
In our case, the class Execution allows you to compose all the elements necessary for the algorithm run and then it performs it and provides you the end results of that execution.
So first, you create an instance ex of Execution.
Then you set the algorithm that should be applied via the method ex.set_algorithm(...).
Then you set the objective function via the method ex.set_objective(...).
Then, via ex.set_solution_space(...) you set the solution space that contains all possible solutions and is explored by the algorithm.
The solution space is an instance of the class Space.
It provides all methods necessary to create a solution data structure, to copy the contents of one solution data structure to another one, to convert solution data structures to and from strings, and to verify whether a solution data structure is valid.
It is used by the optimization algorithm for instantiating the solution data structures and for copying them.
It is used internally by the moptipy system to automatically maintain copies of the current best solution, to check if the solutions are indeed valid once the algorithm finishes, and to convert the solution to a string to store it in the log files.
If the search and solution spaces are different, then you can also set a search space via ex.set_search_space(...) and an encoding via ex.set_encoding(...).
This is not necessary if the algorithm works directly on the solutions (as in our example below).
Each application of an optimization algorithm to a problem instance will also be provided with a random number generator and it must only use this random number generator for randomization and no other sources of randomness.
You can set the seed for this random number generator via ex.set_rand_seed(...).
If you create two identical executions and set the same seeds for both of them, the algorithms will make the same random decisions and hence should return the same results.
Furthermore, you can also set the maximum number of candidate solutions that the optimization algorithm is allowed to investigate via ex.set_max_fes(...), the maximum runtime budget in milliseconds via ex.set_max_time_millis(...), and a goal objective value via ex.set_goal_f(...) (the algorithm should stop after reaching it).
Notice that optimization algorithms may not terminate unless the system tells them to, i.e., unless process.should_terminate() returns True, which is triggered by the termination conditions you define as stated above.
Therefore, you should always specify at least either a maximum number of objective function evaluations or a runtime limit.
If you only specify a goal objective value and the algorithm cannot reach it, it may not terminate.
Finally, you can also set the path to a log file via ex.set_log_file(...).
If you specify a log file, the system will automatically gather system information and collect the end result.
Via ex.set_log_improvements(True), you can instruct the system to also collect the progress of the algorithm in terms of improving moves by default.
In the rare case that you want to log every single move that the algorithm makes, you could call ex.set_log_all_fes(True).
All the collected data will be stored in a text file after the algorithm has completed and you have left the process scope (see below).
Anyway, after you have completed building the execution, you can run the process you have configured via ex.execute().
This method returns an instance of Process.
From the algorithm perspective, this instance provides all the information and tools that is needed to create, copy, and evaluate solutions, as well as the termination criterion that tells it when to stop.
For us, the algorithm user, it provides the information about the end result, the consumed FEs, and the end result quality.
In the code below, we illustrate how to extract these information.
Notice that you must always use the instances of Process in a with block:
Once this block is left, the log file will be written.
If you do not use a with block, no log file will be generated.
Let us now look at a concrete example, which is also available as file examples/single_run_rls_onemax.
As example domain, we use bit strings of length n = 10 and try to solve the well-known OneMax problem using the well-known RLS.
from moptipy.algorithms.so.rls import RLS
from moptipy.api.execution import Execution
from moptipy.examples.bitstrings.onemax import OneMax
from moptipy.operators.bitstrings.op0_random import Op0Random
from moptipy.operators.bitstrings.op1_flip1 import Op1Flip1
from moptipy.spaces.bitstrings import BitStrings
from pycommons.io.temp import temp_file
space = BitStrings(10) # search in bit strings of length 10
problem = OneMax(10) # we maximize the number of 1 bits
algorithm = RLS( # create RLS that
Op0Random(), # starts with a random bit string and
Op1Flip1()) # flips exactly one bit in each step
# We work with a temporary log file which is automatically deleted after this
# experiment. For a real experiment, you would not use the `with` block and
# instead put the path to the file that you want to create into `tf` by doing
# `from pycommons.io.path import Path; tf = Path("mydir/my_file.txt")`.
with temp_file() as tf: # create temporary file `tf`
ex = Execution() # begin configuring execution
ex.set_solution_space(space) # set solution space
ex.set_objective(problem) # set objective function
ex.set_algorithm(algorithm) # set algorithm
ex.set_rand_seed(199) # set random seed to 199
ex.set_log_file(tf) # set log file = temp file `tf`
ex.set_max_fes(100) # allow at most 100 function evaluations
with ex.execute() as process: # now run the algorithm*problem combination
end_result = process.create() # create empty record to receive result
process.get_copy_of_best_y(end_result) # obtain end result
print(f"Best solution found: {process.to_str(end_result)}")
print(f"Quality of best solution: {process.get_best_f()}")
print(f"Consumed Runtime: {process.get_consumed_time_millis()}ms")
print(f"Total FEs: {process.get_consumed_fes()}")
print("\nNow reading and printing all the logged data:")
print(tf.read_all_str()) # instead, we load and print the log file
# The temp file is deleted as soon as we leave the `with` block.The output we would get from this program could look something like this:
Best solution found: TTTTTTTTTT
Quality of best solution: 0
Consumed Runtime: 129ms
Total FEs: 17
Now reading and printing all the logged data:
BEGIN_STATE
totalFEs: 17
totalTimeMillis: 129
bestF: 0
lastImprovementFE: 17
lastImprovementTimeMillis: 129
END_STATE
BEGIN_SETUP
p.name: ProcessWithoutSearchSpace
p.class: moptipy.api._process_no_ss._ProcessNoSS
p.maxFEs: 100
p.goalF: 0
p.randSeed: 199
...
END_SETUP
BEGIN_SYS_INFO
...
END_SYS_INFO
BEGIN_RESULT_Y
TTTTTTTTTT
END_RESULT_Y
You can also compare this output to the example for log files further down this text.
When we develop algorithms or do research, then we cannot just apply an algorithm once to a problem instance and call it a day. Instead, we will apply multiple algorithms (or algorithm setups) to multiple problem instances and execute several runs for each algorithm * instance combination. Our system of course also provides the facilities for this.
The concept for this is rather simple.
We distinguish "instances" and "setups."
An "instance" can be anything that a represents one specific problem instance.
It could be a string with its identifying name, it could be the objective function itself, or a data structure with the instance data (as is the case for the Job Shop Scheduling Problem used in our book, where we use the class Instance).
The important thing is that the __str__ method of the instance object will return a short string that can be used in file names of log files.
The second concept to understand here are "setups."
A "setup" is basically an almost fully configured Execution (see the previous section for a detailed discussion of Executions.)
The only things that need to be left blank are the log file path and random seed, which will be filled automatically by our system.
You will basically provide a sequence of Callables, i.e., functions or lambdas, each of which will return one "instance."
Additionally, you provide a sequence of callables (functions or lambdas), each of which receiving one "instance" as input and should return an almost fully configured Execution.
You also provide the number of runs to be executed per "setup" * "instance" combination and a base directory path identifying the directory where one log file should be written for each run.
moptipy also supports parallel and distributed experiments.
All of this is passed to the function run_experiment in module moptipy.api.experiment.
This function will do all the work and generate a folder structure of log files. It will spawn the right number of processes, use your functions to generate "instances" and "setups," and execute them. It will also automatically determine the random seed for each run. The seed sequence is determined from the instance name using a deterministic procedure and therefore reproducible. The random seed sequence per instance will be the same for all algorithm setups. This means that different algorithms would still start with the same solutions if they sample the first solution in the same way.
The system will even do "warmup" runs, i.e., very short dummy runs with the algorithms that are just used to make sure that the interpreter has seen all code before actually doing the experiments. This avoids situations where the first actual run is slower than the others due to additional interpreter action, i.e., it reduces the bias of time measurements.
Below, we show one example for the automated experiment execution facility, which applies two algorithms to four problem instances with five runs per setup.
We use again the bit strings domain.
We explore two problems (OneMax and LeadingOnes) of two different sizes each, leading to four problem instances in total.
We apply the well-known RLS as well as the trivial random sampling.
The code below is available as file examples/experiment_2_algorithms_4_problems. Besides executing the experiment, it also prints the end results obtained from parsing the log files (see Section 5.2. for more information).
from moptipy.algorithms.so.rls import RLS
from moptipy.algorithms.random_sampling import RandomSampling
from moptipy.api.execution import Execution
from moptipy.api.experiment import run_experiment
from moptipy.evaluation.end_results import from_logs
from moptipy.examples.bitstrings.leadingones import LeadingOnes
from moptipy.examples.bitstrings.onemax import OneMax
from moptipy.operators.bitstrings.op0_random import Op0Random
from moptipy.operators.bitstrings.op1_flip1 import Op1Flip1
from moptipy.spaces.bitstrings import BitStrings
from pycommons.io.temp import temp_dir
# The four problems we want to try to solve:
problems = [lambda: OneMax(10), # 10-dimensional OneMax
lambda: OneMax(32), # 32-dimensional OneMax
lambda: LeadingOnes(10), # 10-dimensional LeadingOnes
lambda: LeadingOnes(32)] # 32-dimensional LeadingOnes
def make_rls(problem) -> Execution:
"""
Create an RLS Execution.
:param problem: the problem (OneMax or LeadingOnes)
:returns: the execution
"""
ex = Execution()
ex.set_solution_space(BitStrings(problem.n))
ex.set_objective(problem)
ex.set_algorithm(RLS( # create RLS that
Op0Random(), # starts with a random bit string and
Op1Flip1())) # flips one bit in each step
ex.set_max_fes(100) # permit 100 FEs
return ex
def make_random_sampling(problem) -> Execution:
"""
Create a Random Sampling Execution.
:param problem: the problem (OneMax or LeadingOnes)
:returns: the execution
"""
ex = Execution()
ex.set_solution_space(BitStrings(problem.n))
ex.set_objective(problem)
ex.set_algorithm(RandomSampling(Op0Random()))
ex.set_max_fes(100)
return ex
# We execute the whole experiment in a temp directory.
# For a real experiment, you would put an existing directory path in `td`
# by doing `from pycommons.io.path import Path; td = directory_path("mydir")`
# and not use the `with` block.
with temp_dir() as td: # create temporary directory `td`
run_experiment(base_dir=td, # set the base directory for log files
instances=problems, # define the problem instances
setups=[make_rls, # provide RLS run creator
make_random_sampling], # provide RS run creator
n_runs=5) # we will execute 5 runs per setup
from_logs( # parse all log files and print end results
td, lambda er: print(f"{er.algorithm} on {er.instance}: {er.best_f}"))
# The temp directory is deleted as soon as we leave the `with` block.The output of this program, minus the status information, could look roughly like this:
rs on onemax_10: 0
rs on onemax_10: 2
rs on onemax_10: 1
rs on onemax_10: 2
rs on onemax_10: 1
rs on onemax_32: 8
rs on onemax_32: 8
rs on onemax_32: 8
rs on onemax_32: 9
rs on onemax_32: 9
rs on leadingones_32: 26
rs on leadingones_32: 26
rs on leadingones_32: 25
rs on leadingones_32: 26
rs on leadingones_32: 23
rs on leadingones_10: 4
rs on leadingones_10: 0
rs on leadingones_10: 3
rs on leadingones_10: 3
rs on leadingones_10: 0
rls_flip1 on onemax_10: 0
rls_flip1 on onemax_10: 0
rls_flip1 on onemax_10: 0
rls_flip1 on onemax_10: 0
rls_flip1 on onemax_10: 0
rls_flip1 on onemax_32: 2
rls_flip1 on onemax_32: 1
rls_flip1 on onemax_32: 2
rls_flip1 on onemax_32: 2
rls_flip1 on onemax_32: 1
rls_flip1 on leadingones_32: 18
rls_flip1 on leadingones_32: 23
rls_flip1 on leadingones_32: 28
rls_flip1 on leadingones_32: 16
rls_flip1 on leadingones_32: 29
rls_flip1 on leadingones_10: 0
rls_flip1 on leadingones_10: 0
rls_flip1 on leadingones_10: 0
rls_flip1 on leadingones_10: 0
rls_flip1 on leadingones_10: 0
You can simply launch the main process several times in parallel in the same folder to achieve parallelism. Actually, you can also execute experiments in a distributed fashion like this: All you have to do is to share the folder for the log files among all computer nodes. Then, in this shared folder, execute the experiment on each node. The system will then automatically ensure that no work is done twice and the experiment runs in a distributed fashion with almost no overhead.
The trick is that we create the random seeds in a deterministic fashion so that each experiment on each node will have the same seeds and, hence, the same names for the log files. The log files are created emptily right before a run starts and filled with data once the run is completed. Since file creation is atomic in distributed file systems, the system can then automatically ensure that no run is performed by more than one node. This is an extremely simple yet very robust method for distribution with very low overhead.
If you want to solve an optimization problem with moptipy, then you need at least the following three things:
- a space
Yof possible solutions, - an objective function
frating the solutions, i.e., which maps elementsyofYto either integer or float numbers, where smaller values are better, and - an optimization algorithm that navigates through
Yand tries to find solutionsyinYwith low corresponding valuesf(y).
You may need more components, but if you have these three, then you can run an experiment.
At the core of all optimization problems lies the objective function.
All objective functions in moptipy are instances of the class Objective.
If you want to add a new optimization problem, you must derive a new subclass from this class.
There are two functions you must be implemented:
evaluate(x)receives a candidate solutionxas input and must return either anintor afloatrating its quality (smaller values are better) and__str__()returns a string representation of the objective function and may be used in file names and folder structures (depending on how you execute your experiments). It therefore must not contain spaces and other dodgy characters.
Additionally, you may implement the following two functions
lower_bound()returns either anintor afloatwith the lower bound of the objective value. This value does not need to be an objective value that can actually be reached, but if you implement this function, then the value must be small enough so that it is impossible to ever reach a smaller objective value. If we execute an experiment and no goal objective value is specified, then the system will automatically use this lower bound if it is present. Then, if any solutionxwithf.evaluate(x)==f.lower_bound()is encountered, the optimization process is automatically stopped. Furthermore, after the optimization process is stopped, it is verified that the final solution does not have an objective value smaller than the lower bound. If it does, then we throw an exception.upper_bound()returns either anintor afloatwith the upper bound of the objective value. This value does not need to be an objective value that can actually be reached, but if you implement this function, then the value must be large enough so that it is impossible to ever reach a larger objective value. This function, if present, is used to validate the objective value of the final result of the optimization process.
OK, with this information we are basically able to implement our own problem.
Here, we define the task "sort n numbers" as optimization problem.
Basically, we want that our optimization algorithm works on permutations of n numbers and is searching for the sorted permutation.
As objective value, we count the number of "sorting errors" in a permutation.
If the number at index i is bigger than the number at index i+1, then this is a sorting error.
If n=5, then the permutation 0;1;2;3;4 has no sorting error, i.e., the best possible objective value 0.
The permutation 4;3;2;1;0 has n-1=4 sorting errors, i.e., is the worst possible solution.
The permutation 3;4;2;0;1 as 2 sorting errors.
From these thoughts, we also know that we can implement lower_bound() to return 0 and upper_bound() to return n-1.
__str__ could be "sort" + n, i.e., sort5 in the above example where n=5.
We provide the corresponding code in Section 3.3.3 below.
While moptipy comes with several well-known algorithms out-of-the-box, you can of course also implement your own algorithms.
These can then make use of the existing spaces and search operators – or not.
Let us here create an example algorithm implementation that does not use any of the pre-defined search operators.
All optimization algorithms must be subclasses of the class Algorithm. Each of them must implement two methods, as described in the documentation:
solve(process)receives an instance ofProcess, which provides the operations to work with the search space, to evaluate solutions, the termination criterion, and the random number generator.__str__()must return a short string representation identifying the algorithm and its setup. This string will be used in file and folder names and therefore must not contain spaces or otherwise dodgy characters.
Additionally, you may need to implement the following methods if the algorithm has other components:
initialize()initializes all sub-components of the algorithms and is called before each run. The base classComponent, from which all elements of the optimization API are derived, already has this method. If a new algorithm uses, for example, a selection algorithm, a temperature schedule, or a search operator, it needs to invoke theinitialize()methods of these components from its owninitialize()method.log_parameters_to(...)is used to store all the configuration parameters of an algorithm to a log section. If the algorithm has any sub-components, it must here invoke thelog_parameters_to(...)method of these components. In this case, it can pass different prefix scopes to thelog_parameters_to(...)methods of its components. Then, different prefixes can be added to each component's parameter keys, ensuring that all keys are unique.
The instance process of Process passed to the function solve is a key element of our moptipy API.
If the algorithm needs a data structure to hold a point in the search space, it should invoke process.create().
If it needs to copy the point source to the point dest, it should invoke process.copy(dest, source).
If it wants to know the quality of the point x, it should invoke process.evaluate(x).
This function will forward the call to the actual objective function (see, e.g., Section 3.3.1 above).
However, it will do more:
It will automatically keep track of the best-so-far solution and, if needed, build logging information in memory.
Before every single call to process.evaluate(), you should invoke process.should_terminate().
This function returns True if the optimization algorithm should stop whatever it is doing and return.
This can happen when a solution of sufficiently good quality is reached, when the maximum number of FEs is exhausted, or when the computational budget in terms of runtime is exhausted.
Since many optimization algorithms make random choices, the function process.get_random() returns a random number generator.
This generator must be the only source of randomness used by an algorithm.
It will automatically be seeded by our system, allowing for repeatable and reproducible runs.
The process also can provide information about the best-so-far solution or point in the search space, the consumed runtime and FEs, as well as when the last improvement was achieved.
Anyway, all interaction between the algorithm and the actual optimization algorithm will happen through the process object.
Equipped with this information, we can develop a simple and rather stupid algorithm to attack the sorting problem.
The search space that we use are the permutations of n numbers.
(These will be internally represented as numpy ndarrays, but we do not need to bother with this, as we this is done automatically for us.)
Our algorithm should start with allocating a point x_cur in the search space, filling it with the numbers 0..n-1, and shuffling it randomly (because we want to start at a random solution).
For the shuffling, it will use than random number generator provided by process.
It will evaluate this solution and remember its quality in variable f_cur.
It will also allocate a second container x_new for permutations.
In each step, our algorithm will copy x_cur to x_new.
Then, it will use the random number generator to draw two numbers i and j from 0..n-1.
It will swap the two numbers at these indices in x_new, i.e., exchange x_new[i], x_new[j] = x_new[j], x_new[i].
We then evaluate x_new and if the resulting objective value f_new is better than f_cur, we swap x_new and x_cur (which is faster than copying x_new to x_cur) and store f_new in f_cur.
We repeat this until process.should_terminate() becomes True.
All of this is implemented in the source code example below in Section 3.3.3.
Finally, as a side note:
Our system can automatically store the results of optimization processes in log file.
The process API also allows your algorithm to store additional information in these files:
First, you can check with process.has_log() if the process was configured to store information in a log file.
If this function returns True, then you can create a section with a given title in the log files that should contain one single string text by calling process.add_log_section(title, text).
Make sure that all section titles are unique.
All such sections will be appended at the end of the log files, wrapped in BEGIN_title and END_title markers, as prescribed by our log file format.
The following code combines our own algorithm and our own problem type that we discussed in the prior two sections and executes an experiment. It is available as file examples/experiment_own_algorithm_and_problem. Notice how we provide functions for generating both the problem instances (here the objective functions) and the algorithm setups exactly as we described in Section 3.2. above.
from moptipy.api.algorithm import Algorithm
from moptipy.api.execution import Execution
from moptipy.api.experiment import run_experiment
from moptipy.api.objective import Objective
from moptipy.api.process import Process
from moptipy.evaluation.end_results import from_logs
from moptipy.spaces.permutations import Permutations
from pycommons.io.temp import temp_dir
class MySortProblem(Objective):
"""An objective function that rates how well a permutation is sorted."""
def __init__(self, n: int) -> None:
"""
Initialize: Set the number of values to sort.
:param n: the scale of the problem
"""
super().__init__()
#: the number of numbers to sort
self.n = n
def evaluate(self, x) -> int:
"""
Compute how often a bigger number follows a smaller one.
:param x: the permutation
"""
errors = 0 # we start at zero errors
for i in range(self.n - 1): # for i in 0..n-2
if x[i] > x[i + 1]: # that's a sorting error!
errors += 1 # so we increase the number
return errors # return result
def lower_bound(self) -> int:
"""
Get the lower bound: 0 errors is the optimum.
Implementing this function is optional, but it can help in two ways:
First, the optimization processes can be stopped automatically when a
solution of this quality is reached. Second, the lower bound is also
checked when the end results of the optimization process are verified.
:returns: 0
"""
return 0
def upper_bound(self) -> int:
"""
Get the upper bound: n-1 errors is the worst.
Implementing this function is optional, but it can help, e.g., when
the results of the optimization process are automatically checked.
:returns: n-1
"""
return self.n - 1
def __str__(self):
"""
Get the name of this problem.
This name is used in the directory structure and file names of the
log files.
:returns: "sort" + n
"""
return f"sort{self.n}"
class MyAlgorithm(Algorithm):
"""An example for a simple rigidly structured optimization algorithm."""
def solve(self, process: Process) -> None:
"""
Solve the problem encapsulated in the provided process.
:param process: the process instance which provides random numbers,
functions for creating, copying, and evaluating solutions, as well
as the termination criterion
"""
random = process.get_random() # get the random number generator
x_cur = process.create() # create the record for the current solution
x_new = process.create() # create the record for the new solution
n = len(x_cur) # get the scale of problem as length of the solution
x_cur[:] = range(n) # We start by initializing the initial solution
random.shuffle(x_cur) # as [0...n-1] and then randomly shuffle it.
f_cur = process.evaluate(x_cur) # compute solution quality
while not process.should_terminate(): # repeat until we are finished
process.copy(x_new, x_cur) # copy current to new solution
i = random.integers(n) # choose the first random index
j = random.integers(n) # choose the second random index
x_new[i], x_new[j] = x_new[j], x_new[i] # swap values at i and j
f_new = process.evaluate(x_new) # evaluate the new solution
if f_new < f_cur: # if it is better than current solution
x_new, x_cur = x_cur, x_new # swap current and new solution
f_cur = f_new # and remember quality of new solution
def __str__(self):
"""
Get the name of this algorithm.
This name is then used in the directory path and file name of the
log files.
:returns: myAlgo
"""
return "myAlgo"
# The four problems we want to try to solve:
problems = [lambda: MySortProblem(5), # sort 5 numbers
lambda: MySortProblem(10), # sort 10 numbers
lambda: MySortProblem(100)] # sort 100 numbers
def make_execution(problem) -> Execution:
"""
Create an application of our algorithm to our problem.
:param problem: the problem (MySortProblem)
:returns: the execution
"""
ex = Execution()
ex.set_solution_space(
Permutations.standard(problem.n)) # we use permutations of [0..n-1]
ex.set_objective(problem) # set the objective function
ex.set_algorithm(MyAlgorithm()) # apply our algorithm
ex.set_max_fes(100) # permit 100 FEs
return ex
# We execute the whole experiment in a temp directory.
# For a real experiment, you would put an existing directory path in `td`
# by doing `from pycommons.io.path import Path; td = directory_path("mydir")`
# and not use the `with` block.
with temp_dir() as td: # create temporary directory `td`
run_experiment(base_dir=td, # set the base directory for log files
instances=problems, # define the problem instances
setups=[make_execution], # creator for our algorithm
n_runs=5) # we will execute 5 runs per setup
from_logs( # parse all log files and print end results
td, lambda er: print(f"{er.algorithm} on {er.instance}: {er.best_f}"))
# The temp directory is deleted as soon as we leave the `with` block.The output of this program, minus status output, could look like this:
myAlgo on sort10: 2
myAlgo on sort10: 2
myAlgo on sort10: 1
myAlgo on sort10: 1
myAlgo on sort10: 2
myAlgo on sort100: 35
myAlgo on sort100: 41
myAlgo on sort100: 33
myAlgo on sort100: 34
myAlgo on sort100: 35
myAlgo on sort5: 1
myAlgo on sort5: 1
myAlgo on sort5: 1
myAlgo on sort5: 1
myAlgo on sort5: 1
Here we list the algorithms, search spaces, and optimization problems that we implement in our moptipy framework.
The following algorithms are completely black-box and work for both single- and multi-objective optimization. (Well, work here is relative … they are basically the worst possible algorithms you could choose and are only included for the sake of completeness.)
- Single Random Sample creates and evaluates exactly one single random solution.
- Random Sampling keeps creating random solutions until the computational budget is exhausted.
- Random Walk creates a random solution and then keeps applying the unary search operator and always accepts the result.
Here we list optimization algorithms that optimize a single objective function.
The first set of algorithms is general, i.e., can work with arbitrary search spaces.
- The simple Hill Climber creates a random solution as initial best-so-far solution and then iteratively applies the unary search operator to the best-so-far solution. When the result of the unary operator is better, it becomes the new best-so-far solution, otherwise it is discarded.
- The Hill Climber with Restarts works exactly like the hill climber, but restarts at a new random solution after a fixed number of unsuccessful moves.
- A Random Local Search (RLS) also known as (1+1) EA works like the Hill Climber as well, but accepts a new solution if it is not worse than the best-so-far solution (instead of requiring it to be strictly better, as the hill climber does).
- The (μ+λ) EA, where "EA" stands for "Evolutionary Algorithm," is a simple population-based metaheuristic that starts with a population of
murandom solutions. In each iteration, it retains only themubest solutions from the population ("best" in terms of the objective value, ties are broken such that newer solutions are preferred). It then applies the unary operator and the binary operator to generatelambdanew solutions and adds them to the population. The(1+1) EAwithbr=0probability to use the binary operator is equivalent to RLS. - The general EA is a generalized version of the (μ+λ) EA that can additionally be configured with a fitness assignment process and both survival and mating selection algorithms.
- Simulated Annealing (SA) is similar to RLS but sometimes accepts worsening moves. The probability to accept such moves gets smaller the worse the moves are and the longer the search continues.
- The (μ+λ) Memetic Algorithm (MA) works like the (μ+λ) EA but it applies the binary search operator at a rate of 100%. (In other words, it never uses the unary search operator). It refines the results of the nullary and binary search operators by using them as starting points of another algorithm, say an SA or RLS, which is executed for a pre-defined number of steps.
- The above MA can be configured to use RLS as local search. This special case is also implemented as hard-coded MA-RLS, which should be a little bit more speed-efficient (due to hard-coding the local search instead of plugging it in), but otherwise it takes the exactly same route through the search space.
- The general MA is a generalized version of the (μ+λ) MA that can additionally be configured with a fitness assignment process and both survival and mating selection algorithms.
- The Plant Propagation Algorithm (PPA) is a population-based metaheuristic that allocates both the number of new solutions to be derived from an existing solution via the unary search operator as well as the step size to be used by this operator based on the normalized objective value of the solution.
The algorithms listed here are intended for single-objective optimization of continuous search spaces.
They only work with search spaces that are instances of VectorSpace.
Such spaces are defined by box-constraints over the n-dimensional real numbers.
- The quasi-Newton method by Broyden, Fletcher, Goldfarb, and Shanno (BFGS), wrapped from SciPy.
- The Bound Optimization BY Quadratic Approximation algorithm (BOBYQA) from the library "Powell's Derivative-Free Optimization solvers" (pdfo).
- The Conjugate Gradient (CG) algorithm, wrapped from SciPy.
- The Covariance Matrix Adaptation Evolution Strategies CMA-ES, Separable CMA-ES, and BIPOP-CMA-ES from the library cmaes.
- Differential Evolution (DE), wrapped from SciPy.
- The Downhill Simplex method based on the Nelder-Mead, wrapped from SciPy.
- Powell's Algorithm, wrapped from SciPy.
- The Sequential Least Squares Programming (SLSQP algorithm, wrapped from SciPy).
- The Truncated Newton Method (TNC), wrapped from SciPy.
The algorithms listed here are suitable for multi-objective optimization. In other words, they try to minimize multiple objective functions at once.
- Multi-Objective Random Local Search (MORLS) works exactly as RLS, but it accepts a solution if it is not dominated by the current solution. This is not a good algorithm.
- The Fast Elitist Non-Dominated Sorting Genetic Algorithm (NSGA-II) is maybe the most popular multi-objective evolutionary algorithm.
- Bit Strings of a fixed length
nare represented asnumpyarrays as well. Here, each value can either beTrueorFalse.- Nullary Operators:
- random initialization fills the string with random bits
- Unary Operators:
- Binary Operators:
- uniform crossover randomly chooses, for each bit, from which of the two source strings it will be copied.
- Nullary Operators:
- Permutations with and without Repetitions are represented as numpy arrays of integers.
A permutation of the values "1,2,3", for example, is an arrangement containing these values in any order.
In
moptipy, the spacePermutationis defined over any arrangement of a given base string. For example, if a base string is "1,2,2,3", then any arrangement containing one "1", two "2"s, and one "3" is then an element of this space. This allows us to represent both normal permutations as well as those with repetitions.- Nullary Operators:
- Fisher-Yates shuffle creates uniformly randomly distributed permutations.
- Unary Operators:
- insert_1 removes one element from a permutation and inserts it elsewhere.
- swap 2 swaps exactly two (different) values.
- swap n performs a random number of swaps.
- swap_exactly_n is a unary operator with step size that will change/swap exactly a given number of elements for permutations where each element occurs once and which will try to swap that many in permutations with repetitions (where it might not be possible to swap exactly the required number of elements).
- swap_try_n is a unary operator very similar to the
swap_exactly_noperator, but it invests much less effort to achieve the number of prescribed swaps and thus is both much faster but also more likely to perform less swaps.
- Binary Operators:
- generalized alternating position crossover chooses, for each index, from which of the two source permutations the (next not-yet-used) value should be copied
- order-based crossover randomly selects a set of indices and copies the elements from first source permutation to the same indices in the destination string. It then copies the remaining elements from the second source, maintaining the order in which they appear in the second source string.
- Nullary Operators:
- Signed Permutations with and without Repetitions are represented as numpy arrays of integers.
They cannot contain the value
0. All other values may occur either positive or negative, e.g.,5or-5.- Nullary Operators:
- shuffle-and-flip creates uniformly randomly distributed signed permutations.
- Unary Operators:
- swap 2 or flip either swaps exactly two (different) values or flips the sign of one value.
- Nullary Operators:
- Ordered Choices are a hybrid of permutations and combinations.
Given are
nchoices, i.e., sets of different values. Each choice could contain any number of different values. Any two choices must either be disjoint or contain the values. Now an element of the space contains one value from each choice and the order matters. So permutations and permutations with repetitions can be represented as ordered choices.- Nullary Operators:
- choose_and_shuffle picks one random value from each choice and shuffles them.
- Nullary Operators:
n-dimensional spaces of real numbers are subsets of then-dimensional real numbers. They arenumpyarrays representing vectors of lengthn. On each dimension, a lower and an upper bound are imposed.- Nullary Operators:
- uniform sampling samples a point from the uniform distribution resulting from the lower- and upper bound of the search space.
- Nullary Operators:
Within this package, we implement a subset of basic problems that are useful for testing different aspects of the algorithms and spaces we provide.
moptipy itself is not intended to be a collection of optimization problems, but more a collection of algorithms, spaces, and operators.
We do need a set of examples to unit test these components, so a set of example problems is indeed provided.
More examples and practical applications of moptipy can be found in the moptipyapps package, which is available on GitHub and in PyPi.
The moptipyapps package is where we will include future examples and benchmark cases, such as for the Quadratic Assignment Problem (QAP), the Traveling Salesperson Problem (TSP), the Traveling Tournament Problem (TTP), Two-Dimensional Bin Packing, or Dynamic Control.
- Bit Strings of a fixed length
n:- The minimization version of the 1D Ising Model, where the goal is to ensure that all bits have the same values as their neighbors.
- The minimization version of the Jump problem, which is equivalent to OneMax, but has a deceptive region right before the optimum.
- The minimization version of the well-known LeadingOnes problem, where the goal is to maximize the length of the trailing substring of all
Truebits. - The minimization version of the well-known OneMax problem, where the goal is to maximize the number of
Truebits in a string. - The minimization version of the Trap problem, which is equivalent of OneMax, but with the optimum and worst-possible solution swapped. This problem is therefore highly deceptive.
- The W-Model, a problem that exhibits tunable neutrality, epistasis, ruggedness, and deceptiveness.
- The minimization version of the well-known ZeroMax problem, which is the exact opposite of OneMax and has the goal to find the bit string of all
Falsevalues.
- Permutations (with and without Repetitions):
- The NP-hard Job Shop Scheduling Problem (JSSP), where the goal is to find an assignment of jobs to machines with the minimum makespan.
On https://thomasweise.github.io/oa_data/, we provide several zip archives with results obtained with
moptipyon the JSSP.
- The NP-hard Job Shop Scheduling Problem (JSSP), where the goal is to find an assignment of jobs to machines with the minimum makespan.
On https://thomasweise.github.io/oa_data/, we provide several zip archives with results obtained with
n-dimensional spaces of real numbers
We develop several data formats to store and evaluate the results of computational experiments with our moptipy software.
Here you can find their basic definitions.
On https://thomasweise.github.io/oa_data/, we provide several zip archives with results obtained with our software.
For example, you could download the results of the hill climber with restarts on the Job Shop Scheduling Problem (JSSP) using the operator swapn that swaps a randomly chosen number of (different) job IDs, for different restart settings.
The files and folders in this archive will then exactly comply to the structure discussed here.
The philosophy of our log files is:
- One log file per algorithm run. We always store each run of an algorithm into a single, separate file. This has several advantages: If you execute several runs in parallel, there cannot be any problems when writing the log files. If, instead, we would store multiple runs in a single file, then some synchronization is needed if multiple processes work on the runs for the same setup. Each log file and run is also self-contained. If runs are executed in a distributed fashion, then we can store data about the node where the run is executed in the log file. We can also store the results of the runs right in the log files without requiring any special treatment to identify to which run the results belong (because there only is one run they could belong to). And so on.
- Each log file contains all information needed to fully understand the algorithm run, such as
- The results in numerical form, e.g., the best achieved objective value.
- The result in textual form, e.g., the textual representation of the best solution discovered This allows us to later load, use, or validate the result.
- The random seed used.
- The termination criteria used, i.e., the maximum objective function evaluations or the maximum runtime or the goal objective value.
- The algorithm name and configuration. This allows us to later understand what we did here and to reproduce the algorithm setup.
- The problem instance name and parameters. This makes sure that we know which problem instance did we solve.
- The system configuration, such as the CPU nd operating system and Python version and library versions. We need to this to understand and reproduce time-dependent measures or to understand situations where changes in the underlying system configuration may have led to different results.
- Errors, if any occurred. We can guard against errors using unit tests, but it may still happen that a run of the optimization algorithm crashed. Our system tries to catch as detailed error information as possible and store it in the log files in order to allow us to figure out what went wrong.
- The progress that the algorithm made over time, if capturing this information was demanded.
- The contents of the archive of non-dominated solutions, if we perform multi-objective optimization.
- The objective values of the solutions in the archive of non-dominated solutions, if we perform multi-objective optimization.
All of this information is stored (almost) automatically.
Experiments with moptipy are intended to be self-documenting, such that you can still see what was going on if you open a log file of someone else or one of your log files five years after the experiment.
Each log file contains all the information, so you will not end up with a situation where you have a "results file" but cannot find the matching setup information because it was stored elsewhere.
By capturing and storing as much information about the setup, configuration, and parameters of each run automatically, we also try to prevent situations where a vital piece of information turns out to be missing some time after the experiment.
For example, the library author himself has encountered situations where he still, e.g., had the result of a run but did not store how long it took to get it.
And did no longer remember when this information was needed.
In such a case we have no choice but to repeat the experiment.
Unless our system is clever enough to automatically store such data.
moptipy is 😁.
One independent run of an algorithm on one problem instance produces one log file.
Each run is identified by the algorithm that is applied, the problem instance to which it is applied, and the random seed.
This tuple is reflected in the file name.
rls_swap2_demo_0x5a9363100a272f12.txt, for example, represents the algorithm rls_swap2 applied to the problem instance demo and started with random seed 0x5a9363100a272f12 (where 0x stands for hexademical notation).
The log files are grouped in a algorithm/instance folder structure.
In the above example, there would be a folder rls_swap2 containing a folder demo, which, in turn, contains all the log files from all runs of that algorithm on this instance.
A log file is a simple text file divided into several sections.
Each section X begins with the line BEGIN_X and ends with the line END_X.
There are three types of sections:
- Semicolon-separated values can hold a series of data values, where each row is divided into multiple values and the values are separated by
;. We use ';', as both '.' and ',' might be misinterpreted as decimal or fractional separaters under different locales, whereas ';', to the best of our knowledge, is rarely used for such purposes. We will still call such sections "CSV" sections (comma-separated-values), though, as most people know what CSV is and the structure basically is exactly that, except that we use ';' instead of ','. - Key-values sections represent, well, values for keys in form of a mapping compatible with YAML.
In other words, each line contains a key, followed by
:, followed by the value. The keys can be hierarchically structured in scopes, for examplea.banda.cindicate two keysbandcthat belong to scopea. This allows representing complex data such as configuration parameters in a rather straight-forward, easy-to-parse canonical way. All keys within a section must be unique, i.e., if a section contains a value under keya.a, it cannot contain the same keya.aagain, even with the same value. - Raw text sections contain text without a general or a priori structure, e.g., the string representation of the best solutions found. Obviously, such raw text cannot contain things such as section delimiters or other reserved keywords. Apart from that, basically any type of data may be stored there. This is useful for, for instance, storing the final solutions of runs or exceptions caught during the runs.
In all the above sections, the character # is removed from output.
The character # indicates a starting comment and can only be written by the routines dedicated to produce comments.
When setting up an algorithm execution, you can specify whether or not you want to log the progress of the algorithm.
If and only if you choose to log the progress, the PROGRESS section will be contained in the log file.
Notice that this section can be long if the algorithm makes many improvements.
You can also choose if you want to log all algorithm steps or only the improving moves, the latter being the default behavior.
If you really log all algorithm steps, then your log files will contain one line for every objective function evaluation (FE) you perform.
It can thus become quite large.
In our Job Shop Scheduling example in the Optimization Algorithms book, for example, we can do several million FEs within the two minutes of runtime granted to each run.
This then would equate to several millions of lines in the PROGRESS section of each log file.
So normally you would rather only log the improving moves, which would often be between a few ten to a few thousand of lines, which is usually acceptable.
Notice that even if you do not choose to log the algorithm's progress at all, the section STATE with the objective value of the best solution encountered, the FE when it was found, and the consumed runtime, as well as the RESULT_* sections with the best encountered candidate solution and point in the search space, and also the SETUP and SYS_INFO still will be included in the log files.
The PROGRESS section contains log points describing the algorithm progress over time in a semicolon-separated values format with one data point per line.
It has an internal header describing the data columns.
There will at least be the following columns:
fesdenoting the integer number of performed objective value evaluationstimeMSthe clock time that has passed since the start of the run, measured in milliseconds and stored as integer value. Python actually provides the system clock time in terms of nanoseconds, however, we always round up to the next highest millisecond. We believe that milliseconds are a more reasonable time measure here and a higher resolution is probably not helpful anyway. Due to the upwards-rounding, the lowest possible time at which a log point can occur is at1millisecond.fthe best-so-far objective value, if only improving moves are logged, or the current objective value, if all moves are logged.
This configuration is denoted by the header fes;timeMS;f.
After this header and until END_PROGRESS, each line will contain one data point with values for the specified columns.
If you perform multi-objective optimization, then one additional column will be added for each objective function.
The column header will be fi with i being the zero-based index of the (i+1th) objective function.
f then stands for the scalarized version of the objective values.
You can copy the contents of this section together with the header into calculation software such as Microsoft Excel or LibreOffice Calc and choose ; as separator when applying the text-to-column feature.
This way, you can directly work on the raw data if you want.
Notice that for each FE, there will be at most one data point but there might be multiple data points per millisecond. This is especially true if we log all FEs. Usually, we would log one data point for every improvement of the objective value, though.
The end state when the run terminates is logged in the section STATE in a YAML-compatible key-value format.
It holds at least the following keys:
totalFEsthe total number of objective function evaluations performed, as integertotalTimeMillisthe total number of clock time milliseconds elapsed since the begin of the run, as integerbestFthe best objective function value encountered during the runlastImprovementFEthe index of the last objective function evaluation where the objective value improved, as integerlastImprovementTimeMillisthe time in milliseconds at which the last objective function value improvement was registered, as integer
In case that multi-objective optimization is performed, please note the following things:
bestFthen corresponds to the best scalarization result, i.e., the best value achieved by the scalarization of the objective value vector during the search,bestFs, the vector of objective values corresponding to the solution obtainingbestF, is also provided (values are semicolon-separated),archiveSizeis the number of non-dominated solutions collected in the archive, and- the values of
lastImprovementFEandlastImprovementTimeMillismay not be reliable anymore: Whenever a solution enters the archive or the best scalarization is improved, this is recorded as improvement. However, since the archive size is always limited and the archive may be pruned due when it reaches its maximum size, it could be that a solution enters the archive which is actually not non-dominated with respect to the whole search but only with respect to the current archive. In other words,lastImprovementFEandlastImprovementTimeMillismay represent a move that is actually not an absolute improvement.
In this YAML-compatible key-value section, we log information about the configuration of the optimization algorithm as well as the parameters of the problem instance solved. There are at least the following keys:
- process wrapper parameters (scope
p):p.name: the name of the process wrapper, i.e., a short mnemonic describing its purposep.class: the python class of the process wrapperp.maxTimeMillis: the maximum clock time in milliseconds, if specifiedp.maxFEs: the maximum number of objective function evaluations (FEs), if specifiedp.goalF: the goal objective value, if specified (or computed via thelower_bound()of the objective function)p.randSeed: the random seed (a 64bit unsigned integer) in decimal notationp.randSeed(hex): the random seed in hexadecimal notationp.randGenType: the class of the random number generatorp.randBitGenType: the class of the bit generator used by the random number generatorp.lowerBoundthe lower bound of the (scalarized) objective values that this process can produce (if finite)p.upperBoundthe upper bound of the (scalarized) objective values that this process can produce (if finite) If multi-objective optimization is performed, the following parameters are added:p.archiveMaxSize: the maximum size of the archive of non-dominated solutions after pruningp.archivePruneLimit: the archive size limit above which pruning will be triggered.
- algorithm parameters: scope
a, includes algorithmname,class, etc. - solution space scope
y, includesnameandclassof solution space - objective function information: scope
f. If multi-objective optimization is performed, this is the scope of the multi-objective problem. There will be a sub-scopef.fifor theith objective function (istarts at0). - search space information (if search space is different from solution space): scope
x - encoding information (if encoding is defined): scope
g - archive pruner information (in case of multi-objective optimization): scope
ap.
If you implement an own algorithm, objective function, space, or your own search operators, then you can overwrite the method log_parameters_to(logger).
This method will automatically be invoked when writing the log files of a run.
It should always start with calling the super implementation (super().log_parameters_to(logger)).
After that, you can store key-value pairs describing the parameterization of your component.
This way, such information can be preserved in log files.
We strongly suggest to always do that if you define your own components. It is a very easy way to make sure that your results are reproducible, easy-to-understand, and self-documenting.
The system information section is again a key-value section.
It holds key-value pairs describing features of the machine on which the experiment was executed.
This includes information about the CPU, the operating system, the Python installation, as well as the version information of packages used by moptipy.
If your moptipy application uses additional Python libraries, then it is strongly suggested to also include their versions in the log files.
This can be done by invoking the function add_dependency before running any experiment.
This way, you can add the name of a library that your application depends on.
The system will then automatically get the version information of that library and include it into the log files.
The textual representation of the best encountered solution (whose objective value is noted as bestF in section STATE) is stored in the section RESULT_Y.
Since we can use many different solution spaces, this section just contains raw text.
If the search and solution space are different, the section RESULT_X is included.
It then holds the point in the search space corresponding to the solution presented in RESULT_Y.
Both sections are plain texts, the results of the to_str method of the corresponding Space instances for the search and solution spaces.
It is therefore possible to design suitable text representations for arbitrary solution data structures and have them properly stored in the log files.
Our package has mechanisms to catch and store errors that occurred during the experiments.
Each type of error will be stored in a separate log section and each such sections may store the class of the error in form exceptionType: error-class, the error message in the form exceptionValue: error-message and the stack trace line by line after a line header exceptionStackTrace:.
The following exception sections are currently supported:
- If an exception is encountered during the algorithm run, it will be store in section
ERROR_IN_RUN. - If an exception occurred in the context of the optimization process, it will be stored in
ERROR_IN_CONTEXT. This may be an error during the execution of the algorithm, or, more likely, an error in the code that accesses the process data afterwards, e.g., that processes the best solution encountered. - If the validation of the finally returned candidate solution failed, the resulting error will be stored in section
ERROR_INVALID_Y. - If the internally remembered best objective value does not match to the objective value of the internally remembered best solution after re-evaluating it at the end, the corresponding information will be stored in section
ERROR_BEST_F_MISMATCH. - If the validation of the finally returned point in the search space failed, the resulting error will be stored in section
ERROR_INVALID_X. - If an inconsistency in the time measurement is discovered, this will result in the section
ERROR_TIMING. Such an error may be caused when the computer clock is adjusted during the run of an optimization algorithm. It will also occur if an algorithm terminates without performing even a single objective function evaluation. - In the unlikely case that an exception occurs during the writing of the log but writing can somehow continue, this exception will be stored in section
ERROR_IN_LOG.
If multi-objective optimization is performed, the process object will automatically collect an archive of non-dominated solutions.
In the CSV-formatted section ARCHIVE_QUALITIES of the log files, we will find one row per non-dominated solution in the archive.
The first number in the row is the scalarized overall solution quality f, followed by the value fi of the ith objective function (i starts at 0).
The solutions corresponding to row j of this section appear in the ARCHIVE_j_X and ARCHIVE_j_Y sections (j starts at 0).
In multi-objective optimization, the process object will automatically collect an archive of non-dominated solutions.
The sections ARCHIVE_j_X contains the point in the search space and ARCHIVE_j_Y the point in the solution space corresponding to the jth element of the archive.
The sections are plain texts, the results of the to_str method of the corresponding Space instances for the search and solution spaces.
You can execute the following Python code to obtain an example log file. This code is also available in file examples/log_file_jssp.py:
from moptipy.algorithms.so.rls import RLS # the algorithm we use
from moptipy.examples.jssp.experiment import run_experiment # the runner
from moptipy.operators.permutations.op0_shuffle import Op0Shuffle # 0-ary op
from moptipy.operators.permutations.op1_swap2 import Op1Swap2 # 1-ary op
from pycommons.io.temp import temp_dir # temp directory tool
# We work in a temporary directory, i.e., delete all generated files on exit.
# For a real experiment, you would put an existing directory path in `td`
# by doing `from pycommons.io.path import Path; td = directory_path("mydir")`
# and not use the `with` block.
with temp_dir() as td: # create temp directory
# Execute an experiment consisting of exactly one run.
# As example domain, we use the job shop scheduling problem (JSSP).
run_experiment(
base_dir=td, # working directory = temporary directory
algorithms=[ # the set of algorithms to use: we use only 1
# an algorithm is created via a lambda
lambda inst, pwr: RLS(Op0Shuffle(pwr), Op1Swap2())],
instances=("demo",), # use the demo JSSP instance
n_runs=1) # perform exactly one run
# The random seed is automatically generated based on the instance name.
print(td.resolve_inside( # so we know algorithm, instance, and seed
"rls_swap2/demo/rls_swap2_demo_0x5a9363100a272f12.txt")
.read_all_str()) # read file into string (which then gets printed)
# When leaving "while", the temp directory will be deletedThe example log file printed by the above code will then look something like this:
BEGIN_PROGRESS
fes;timeMS;f
1;1;267
5;1;235
10;1;230
20;1;227
25;1;205
40;1;200
84;2;180
END_PROGRESS
BEGIN_STATE
totalFEs: 84
totalTimeMillis: 2
bestF: 180
lastImprovementFE: 84
lastImprovementTimeMillis: 2
END_STATE
BEGIN_SETUP
p.name: LoggingProcessWithSearchSpace
p.class: moptipy.api._process_ss_log._ProcessSSLog
p.maxTimeMillis: 120000
p.goalF: 180
p.randSeed: 6526669205530947346
p.randSeed(hex): 0x5a9363100a272f12
p.randGenType: numpy.random._generator.Generator
p.randBitGenType: numpy.random._pcg64.PCG64
a.name: rls_swap2
a.class: moptipy.algorithms.rls.RLS
a.op0.name: shuffle
a.op0.class: moptipy.operators.permutations.op0_shuffle.Op0Shuffle
a.op1.name: swap2
a.op1.class: moptipy.operators.permutations.op1_swap2.Op1Swap2
y.name: gantt_demo
y.class: moptipy.examples.jssp.gantt_space.GanttSpace
y.shape: (5, 4, 3)
y.dtype: h
y.inst.name: demo
y.inst.class: moptipy.examples.jssp.instance.Instance
y.inst.machines: 5
y.inst.jobs: 4
y.inst.makespanLowerBound: 180
y.inst.makespanUpperBound: 482
y.inst.dtype: b
f.name: makespan
f.class: moptipy.examples.jssp.makespan.Makespan
x.name: perm4w5r
x.class: moptipy.spaces.permutations.Permutations
x.nvars: 20
x.dtype: b
x.min: 0
x.max: 3
x.repetitions: 5
g.name: operation_based_encoding
g.class: moptipy.examples.jssp.ob_encoding.OperationBasedEncoding
g.dtypeMachineIdx: b
g.dtypeJobIdx: b
g.dtypeJobTime: h
END_SETUP
BEGIN_SYS_INFO
session.start: 2022-05-03 08:49:14.883057+00:00
session.node: home
session.procesId: 0xc4b9
session.cpuAffinity: 0;1;2;3;4;5;6;7;8;9;10;11;12;13;14;15
session.ipAddress: 192.168.1.105
version.moptipy: 0.8.5
version.numpy: 1.21.5
version.numba: 0.55.1
version.matplotlib: 3.5.1
version.psutil: 5.9.0
version.scikitlearn: 1.0.2
hardware.machine: x86_64
hardware.nPhysicalCpus: 8
hardware.nLogicalCpus: 16
hardware.cpuMhz: (2200MHz..3700MHz)*16
hardware.byteOrder: little
hardware.cpu: AMD Ryzen 7 2700X Eight-Core Processor
hardware.memSize: 16719478784
python.version: 3.10.4 (main, Apr 2 2022, 09:04:19) [GCC 11.2.0]
python.implementation: CPython
os.name: Linux
os.release: 5.15.0-27-generic
os.version: 28-Ubuntu SMP Thu Apr 14 04:55:28 UTC 2022
END_SYS_INFO
BEGIN_RESULT_Y
1;20;30;0;30;40;3;145;165;2;170;180;1;0;20;0;40;60;2;60;80;3;165;180;2;0;30;0;60;80;1;80;130;3;130;145;1;30;60;3;60;90;0;90;130;2;130;170;3;0;50;2;80;92;1;130;160;0;160;170
END_RESULT_Y
BEGIN_RESULT_X
2;1;3;1;0;0;2;0;1;2;3;1;0;2;1;3;0;3;2;3
END_RESULT_X
You can execute the following Python code to obtain an example log file for multi-objective optimization.
Under moptipy, every multi-objective problem also specifies a default scalarization, making it and its log files compatible with single-objective optimization.
The optimization algorithms can, however, perform Pareto optimization, which is fully respected and whose archive of non-dominated solutions are stored in the log files.
This code is also available in file examples/mo_example_nsga2_bits.py:
from moptipy.algorithms.mo.nsga2 import NSGA2
from moptipy.api.mo_execution import MOExecution
from moptipy.examples.bitstrings.leadingones import LeadingOnes
from moptipy.examples.bitstrings.zeromax import ZeroMax
from moptipy.mo.problem.weighted_sum import WeightedSum
from moptipy.operators.bitstrings.op0_random import Op0Random
from moptipy.operators.bitstrings.op1_flip1 import Op1Flip1
from moptipy.operators.bitstrings.op2_uniform import Op2Uniform
from moptipy.spaces.bitstrings import BitStrings
from pycommons.io.temp import temp_file
solution_space = BitStrings(16) # We search a bit string of length 16,
f1 = ZeroMax(16) # that has as many 0s in it as possible
f2 = LeadingOnes(16) # and the longest leading sequence of 1s.
# These are, of course, two conflicting goals.
# Each multi-objective optimization problem is defined by several objective
# functions *and* a way to scalarize the vector of objective values.
# The scalarization is only used by the system to decide for one single best
# solution in the end *and* if we actually apply a single-objective algorithm
# to the problem instead of a multi-objective one. (Here we will apply a
# multi-objective algorithm, though.)
# Here, we decide for a weighted sum scalarization, weighting the number of
# zeros half as much as the number of leading ones.
problem = WeightedSum([f1, f2], [1, 2])
# NSGA-II is the most well-known multi-objective optimization algorithm.
# It works directly on the multiple objectives. It does not require the
# scalarization above at all. The scalarization is _only_ used internally in
# the `Process` objects to ensure compatibility with single-objective
# optimization and for being able to remember a single "best" solution.
algorithm = NSGA2( # Create the NSGA-II algorithm.
Op0Random(), # start with a random bit string and
Op1Flip1(), # flips single bits as mutation
Op2Uniform(), # performs uniform crossover
10, 0.05) # population size = 10, crossover rate = 0.05
# We work with a temporary log file which is automatically deleted after this
# experiment. For a real experiment, you would not use the `with` block and
# instead put the path to the file that you want to create into `tf` by doing
# `from pycommons.io.path import Path; tf = Path("mydir/my_file.txt")`.
with temp_file() as tf: # create temporary file `tf`
ex = MOExecution() # begin configuring execution
ex.set_solution_space(solution_space)
ex.set_objective(problem) # set the multi-objective problem
ex.set_algorithm(algorithm)
ex.set_rand_seed(200) # set random seed to 200
ex.set_log_improvements(True) # log all improving moves
ex.set_log_file(tf) # set log file = temp file `tf`
ex.set_max_fes(300) # allow at most 300 function evaluations
with ex.execute(): # now run the algorithm*problem combination
pass
print("\nNow reading and printing all the logged data:")
print(tf.read_all_str()) # instead, we load and print the log file
# The temp file is deleted as soon as we leave the `with` block.The example log file printed by the above code will then look something like this:
BEGIN_PROGRESS
fes;timeMS;f;f0;f1
1;1;36;6;15
6;1;37;9;14
7;1;37;5;16
8;1;36;10;13
13;2;36;8;14
14;2;35;3;16
19;2;35;7;14
21;2;35;5;15
22;2;35;9;13
27;3;34;6;14
31;3;34;8;13
33;3;32;10;11
42;4;33;7;13
46;4;34;2;16
50;4;27;11;8
57;5;31;9;11
64;6;32;6;13
67;6;33;3;15
72;6;31;5;13
75;6;33;1;16
77;6;32;8;12
78;7;32;4;14
79;7;24;12;6
82;7;23;11;6
84;7;32;0;16
88;7;30;8;11
91;8;30;4;13
93;8;31;3;14
101;9;30;10;10
112;9;26;10;8
114;10;32;2;15
118;10;24;10;7
126;10;29;7;11
131;11;22;10;6
133;11;28;8;10
139;11;31;1;15
147;12;23;9;7
161;13;28;6;11
181;15;26;8;9
187;15;29;5;12
191;15;30;2;14
244;19;21;11;5
260;20;27;5;11
293;23;25;7;9
END_PROGRESS
BEGIN_STATE
totalFEs: 300
totalTimeMillis: 23
bestF: 21
lastImprovementFE: 293
lastImprovementTimeMillis: 23
bestFs: 11;5
archiveSize: 9
END_STATE
BEGIN_SETUP
p.name: MOLoggingProcessWithoutSearchSpace
p.class: moptipy.api._mo_process_no_ss_log._MOProcessNoSSLog
p.lowerBound: 0
p.upperBound: 48
p.maxFEs: 300
p.goalF: 0
p.randSeed: 200
p.randSeed(hex): 0xc8
p.randGenType: numpy.random._generator.Generator
p.randBitGenType: numpy.random._pcg64.PCG64
p.archiveMaxSize: 32
p.archivePruneLimit: 128
a.name: nsga2_10_0d05_uniform_flip1
a.class: moptipy.algorithms.mo.nsga2.NSGA2
a.op0.name: randomize
a.op0.class: moptipy.operators.bitstrings.op0_random.Op0Random
a.op1.name: flip1
a.op1.class: moptipy.operators.bitstrings.op1_flip1.Op1Flip1
a.op2.name: uniform
a.op2.class: moptipy.operators.bitstrings.op2_uniform.Op2Uniform
a.pop_size: 10
a.cr: 0.05
a.cr(hex): 0x1.999999999999ap-5
y.name: bits16
y.class: moptipy.spaces.bitstrings.BitStrings
y.nvars: 16
y.dtype: ?
f.name: weightedSum
f.class: moptipy.mo.problem.weighted_sum.WeightedSum
f.lowerBound: 0
f.upperBound: 48
f.nvars: 2
f.dtype: b
f.f0.name: zeromax_16
f.f0.class: moptipy.examples.bitstrings.zeromax.ZeroMax
f.f0.lowerBound: 0
f.f0.upperBound: 16
f.f0.n: 16
f.f1.name: leadingones_16
f.f1.class: moptipy.examples.bitstrings.leadingones.LeadingOnes
f.f1.lowerBound: 0
f.f1.upperBound: 16
f.f1.n: 16
f.weights: 1;2
f.weightsDtype: b
ap.name: keepFarthest
ap.class: moptipy.mo.archive.keep_farthest.KeepFarthest
END_SETUP
BEGIN_SYS_INFO
session.start: 2023-02-18 07:28:08.247748+00:00
session.node: home
session.procesId: 0x2d20b
session.cpuAffinity: 0;1;2;3;4;5;6;7;8;9;10;11;12;13;14;15
session.ipAddress: 192.168.1.109
version.moptipy: 0.9.53
version.contourpy: 1.0.6
version.cycler: 0.11.0
version.fonttools: 4.38.0
version.joblib: 1.2.0
version.kiwisolver: 1.4.4
version.llvmlite: 0.39.1
version.matplotlib: 3.7.0
version.numba: 0.56.4
version.numpy: 1.23.5
version.packaging: 21.3
version.pdfo: 1.2
version.Pillow: 9.4.0
version.psutil: 5.9.4
version.pyparsing: 3.0.9
version.pythondateutil: 2.8.2
version.scikitlearn: 1.2.1
version.scipy: 1.10.0
version.six: 1.16.0
version.threadpoolctl: 3.1.0
hardware.machine: x86_64
hardware.nPhysicalCpus: 8
hardware.nLogicalCpus: 16
hardware.cpuMhz: (2200MHz..3700MHz)*16
hardware.byteOrder: little
hardware.cpu: AMD Ryzen 7 2700X Eight-Core Processor
hardware.memSize: 16717656064
python.version: 3.10.6 (main, Nov 14 2022, 16:10:14) [GCC 11.3.0]
python.implementation: CPython
os.name: Linux
os.release: 5.19.0-32-generic
os.version: 33~22.04.1-Ubuntu SMP PREEMPT_DYNAMIC Mon Jan 30 17:03:34 UTC 2
END_SYS_INFO
BEGIN_RESULT_Y
TTTTTTTTTTTFFFFF
END_RESULT_Y
BEGIN_ARCHIVE_0_Y
FFFFFFFFFFFFFFFF
END_ARCHIVE_0_Y
BEGIN_ARCHIVE_1_Y
TFFFFFFFFFFFFFFF
END_ARCHIVE_1_Y
BEGIN_ARCHIVE_2_Y
TTFFFFFFFFFFFFFF
END_ARCHIVE_2_Y
BEGIN_ARCHIVE_3_Y
TTTFFFFFFFFFFFFT
END_ARCHIVE_3_Y
BEGIN_ARCHIVE_4_Y
TTTTTFFFFFFFFFFF
END_ARCHIVE_4_Y
BEGIN_ARCHIVE_5_Y
TTTTTTTFFFFFFFFF
END_ARCHIVE_5_Y
BEGIN_ARCHIVE_6_Y
TTTTTTTTTFFFFFFF
END_ARCHIVE_6_Y
BEGIN_ARCHIVE_7_Y
TTTTTTTTTTFFFFFF
END_ARCHIVE_7_Y
BEGIN_ARCHIVE_8_Y
TTTTTTTTTTTFFFFF
END_ARCHIVE_8_Y
BEGIN_ARCHIVE_QUALITIES
f;f0;f1
32;0;16
31;1;15
30;2;14
30;4;13
27;5;11
25;7;9
23;9;7
22;10;6
21;11;5
END_ARCHIVE_QUALITIES
While a log file contains all the data of a single run, you often want to get just the basic measurements, such as the result objective values, from all runs of one experiment in a single file.
The class moptipy.evaluation.end_results.EndResult provides the tools needed to parse all log files, extract these information, and store them into a semicolon-separated-values formatted file.
The files generated this way can easily be imported into applications like Microsoft Excel.
If you have the moptipy package installed, then you can call the module directly from the command line as:
python3 -m moptipy.evaluation.end_results source_dir dest_filewhere source_dir should be the root directory with the experimental data (see Section 5.1.1)) and dest_file is the path to the CSV file to write.
An end results file contains a header line and then one line for each log file that was parsed.
The eleven columns are separated by ;.
Cells without value are left empty.
It presents the following columns:
algorithm: the algorithm that was executedinstance: the instance it was applied toobjective: the name of the objective function- optionally
encoding: the name of the encoding, if any encoding was used. This column is omitted if the search and solution space was the same in all runs and no encoding was used. If at least one run did use an encoding, this column is present. It will contain nothing for the runs that did not use an encoding. randSeedthe hexadecimal version of the random seed of the runbestF: the best objective value encountered during the runlastImprovementFE: the FE when the last improvement was registeredlastImprovementTimeMillis: the time in milliseconds from the start of the run when the last improvement was registeredtotalFEs: the total number of FEs performedtotalTimeMillis: the total time in milliseconds consumed by the run- optionally
goalF: the goal objective value, if specified, otherwise omitted. If at least one run specified a goal objective value, this column is present. Otherwise it is omitted. For runs not having a goal objective value, it remains empty. - optionally
maxFEs: the computational budget in terms of the maximum number of permitted FEs, if specified, otherwise omitted. If at least one run specified a time limit in terms of objective function evaluations, this column is present. Otherwise it is omitted. For runs not having an FE-based time limit, it remains empty. - optionally
maxTimeMillis: the computational budget in terms of the maximum runtime in milliseconds, if specified, otherwise omitted. If at least one run specified a time limit in terms of milliseconds, this column is present. Otherwise it is omitted. For runs not having a ms-based time limit, it remains empty.
For each run, i.e., "algorithm x instance x seed combination," one row with the above values is generated. Notice that from the algorithm and instance name together with the random seed, you can find the corresponding log file. In some situations, you may apply "algorithm x instance x seed combinations" together with different objective functions or different encodings or both. In such situations, you would store the results in different base folders, as these elements do not appear in the algorithm names. They are contained in the end results CSV file, though.
Let us execute an abridged example experiment, parse all log files, condense their information into an end results statistics file, and then print that file's contents. We can do that with the code below, which is also available as file examples/end_results_jssp.py.
"""Generate an end-results CSV file for an experiment with the JSSP."""
from pycommons.io.temp import temp_dir # tool for temp directories
from moptipy.algorithms.so.hill_climber import HillClimber # second algo
from moptipy.algorithms.so.rls import RLS # first algo to test
from moptipy.evaluation.end_results import from_logs, to_csv # end results
from moptipy.examples.jssp.experiment import run_experiment # JSSP example
from moptipy.operators.permutations.op0_shuffle import Op0Shuffle # 0-ary op
from moptipy.operators.permutations.op1_swap2 import Op1Swap2 # 1-ary op
# We work in a temporary directory, i.e., delete all generated files on exit.
# For a real experiment, you would put an existing directory path into `td` by
# doing `from pycommons.io.path import Path; td = Path("mydir")` and not use
# the `with` block.
with temp_dir() as td:
run_experiment( # run the JSSP experiment with the following parameters:
base_dir=td, # base directory to write all log files to
algorithms=[ # the set of algorithm generators
lambda inst, pwr: RLS(Op0Shuffle(pwr), Op1Swap2()), # algo 1
lambda inst, pwr: HillClimber(Op0Shuffle(pwr), Op1Swap2())], # 2
instances=("demo", "abz7", "la24"), # we use 3 JSSP instances
max_fes=10000, # we grant 10000 FEs per run
n_runs=4) # perform 4 runs per algorithm * instance combination
end_results = [] # this list will receive the end results records
from_logs(td, end_results.append) # get results from log files
er_csv = to_csv( # store end results to csv file (returns path)
end_results, # the list of end results to store
td.resolve_inside("end_results.txt")) # path to the file to generate
print(er_csv.read_all_str()) # read generated file as string and print it
# When leaving "while", the temp directory will be deletedThis will yield something like the following output:
# Experiment End Results
# See the description at the bottom of the file.
algorithm;instance;objective;encoding;randSeed;bestF;lastImprovementFE;lastImprovementTimeMillis;totalFEs;totalTimeMillis;goalF;maxFEs;maxTimeMillis
hc_swap2;abz7;makespan;operation_based_encoding;0x3e96d853a69f369d;826;8335;56;10000;67;656;10000;300000
hc_swap2;abz7;makespan;operation_based_encoding;0x7e986b616543ff9b;850;6788;52;10000;88;656;10000;300000
hc_swap2;abz7;makespan;operation_based_encoding;0xd3de359d5e3982fd;814;4437;50;10000;87;656;10000;300000
hc_swap2;abz7;makespan;operation_based_encoding;0xeb6420da7243abbe;804;3798;42;10000;111;656;10000;300000
hc_swap2;demo;makespan;operation_based_encoding;0xd2866f0630434df;185;128;2;10000;66;180;10000;300000
hc_swap2;demo;makespan;operation_based_encoding;0x5a9363100a272f12;200;33;1;10000;80;180;10000;300000
hc_swap2;demo;makespan;operation_based_encoding;0x9ba8fd0486c59354;180;34;1;34;1;180;10000;300000
hc_swap2;demo;makespan;operation_based_encoding;0xdac201e7da6b455c;205;4;1;10000;94;180;10000;300000
hc_swap2;la24;makespan;operation_based_encoding;0x23098fe72e435030;1065;9868;98;10000;99;935;10000;300000
hc_swap2;la24;makespan;operation_based_encoding;0xac5ca7763bbe7138;1233;2349;22;10000;97;935;10000;300000
hc_swap2;la24;makespan;operation_based_encoding;0xb4eab9a0c2193a9e;1111;2594;25;10000;98;935;10000;300000
hc_swap2;la24;makespan;operation_based_encoding;0xb76a45e4f8b431ae;1118;2130;13;10000;58;935;10000;300000
rls_swap2;abz7;makespan;operation_based_encoding;0x3e96d853a69f369d;761;9663;92;10000;95;656;10000;300000
rls_swap2;abz7;makespan;operation_based_encoding;0x7e986b616543ff9b;767;9935;80;10000;80;656;10000;300000
rls_swap2;abz7;makespan;operation_based_encoding;0xd3de359d5e3982fd;762;9128;77;10000;82;656;10000;300000
rls_swap2;abz7;makespan;operation_based_encoding;0xeb6420da7243abbe;756;8005;52;10000;64;656;10000;300000
rls_swap2;demo;makespan;operation_based_encoding;0xd2866f0630434df;180;63;1;63;1;180;10000;300000
rls_swap2;demo;makespan;operation_based_encoding;0x5a9363100a272f12;180;84;1;84;1;180;10000;300000
rls_swap2;demo;makespan;operation_based_encoding;0x9ba8fd0486c59354;180;33;1;33;1;180;10000;300000
rls_swap2;demo;makespan;operation_based_encoding;0xdac201e7da6b455c;180;83;1;83;1;180;10000;300000
rls_swap2;la24;makespan;operation_based_encoding;0x23098fe72e435030;1026;9114;91;10000;99;935;10000;300000
rls_swap2;la24;makespan;operation_based_encoding;0xac5ca7763bbe7138;1015;9451;94;10000;99;935;10000;300000
rls_swap2;la24;makespan;operation_based_encoding;0xb4eab9a0c2193a9e;1033;7503;74;10000;98;935;10000;300000
rls_swap2;la24;makespan;operation_based_encoding;0xb76a45e4f8b431ae;1031;5218;30;10000;63;935;10000;300000
# Records describing the end results of single runs (single executions) of algorithms applied to optimization problems.
# Each run is characterized by an algorithm setup, a problem instance, and a random seed.
# algorithm: the name of the algorithm setup that was used.
# instance: the name of the problem instance to which the algorithm was applied.
# objective: the name of the objective function (often also called fitness function or cost function) that was used to rate the solution quality.
# encoding: the name of the encoding, often also called genotype-phenotype mapping, used. In some problems, the search space on which the algorithm works is different from the space of possible solutions. For example, when solving a scheduling problem, maybe our optimization algorithm navigates in the space of permutations, but the solutions are Gantt charts. The encoding is the function that translates the points in the search space (e.g., permutations) to the points in the solution space (e.g., Gantt charts). Nothing if no encoding was used.
# randSeed: the value of the seed of the random number generator used in the run. Random seeds arein 0..18446744073709551615 and the random number generators are those from numpy.
# bestF: the best (smallest) objective value ever encountered during the run (regardless whether the algorithm later forgot it again or not).
...
We can also aggregate the end result data over either algorithm x instance combinations, over whole algorithms, over whole instances, or just over everything.
The class moptipy.evaluation.end_statistics.EndStatistics provides the tools needed to aggregate statistics over sequences of moptipy.evaluation.end_results.EndResult and to store them into a semicolon-separated-values formatted file.
The files generated this way can easily be imported into applications like Microsoft Excel.
If you have the moptipy package installed, then you can call the module directly from the command line as:
python3 -m moptipy.evaluation.end_statistics source dest_filewhere source should either be the root directory with the experimental data (see Section 5.1.1)) or the path to a end results CSV file and dest_file is the path to the CSV file to write.
End result statistics files contain information in form of statistics aggregated over several runs. Therefore, they first contain columns identifying the data over which has been aggregated:
algorithm: the algorithm used (empty if we aggregate over all algorithms)instance: the instance to which it was applied (empty if we aggregate over all instance)
Then the column n denotes the number of runs that were performed in the above setting.
We have then the following data columns:
bestF.x: statistics about the best objective value encountered during the runlastImprovementFE.x: statistics about the index of the objective function evaluation (FE) when the last improvement was registeredlastImprovementTimeMillis.x: statistics about the time in milliseconds from the start of the run when the last improvement was registeredtotalFEs.x: statistics about the total number of FEs performed by the runstotalTimeMillis.x: statistics about the total time in milliseconds consumed by the runs
Here, the .x can stand for the following statistics:
min: the minimummed: the medianmean: the meangeom: the geometric meanmax: the maximumsd: the standard deviation
The column goalF denotes the goal objective value, if any.
If it is not empty and greater than zero, then we also have the columns bestFscaled.x, which provide statistics of bestF/goalF as discussed above.
If goalF is defined for at least some settings, we also get the following columns:
nSuccesses: the number of runs that were successful in reaching the goalsuccessFEs.x: the statistics about the FEs until success, but only computed over the successful runssuccessTimeMillis.x: the statistics of the runtime until success, but only computed over the successful runsertFEs: the empirically estimated runtime to success in FEsertTimeMillis: the empirically estimated runtime to success in milliseconds
Finally, the columns maxFEs and maxTimeMillis, if specified, include the computational budget limits in terms of FEs or milliseconds.
We can basically execute the same abridged experiment as in the previous section, but now take the aggregation of information one step further with the code below. This code is also available as file examples/end_statistics_jssp.
"""Get an end-result statistics CSV file for an experiment with the JSSP."""
from pycommons.io.temp import temp_dir # tool for temp directories
from moptipy.algorithms.so.hill_climber import HillClimber # second algo
from moptipy.algorithms.so.rls import RLS # first algo to test
from moptipy.evaluation.end_results import from_logs # the end result record
from moptipy.evaluation.end_statistics import from_end_results, to_csv
from moptipy.examples.jssp.experiment import run_experiment # JSSP example
from moptipy.operators.permutations.op0_shuffle import Op0Shuffle # 0-ary op
from moptipy.operators.permutations.op1_swap2 import Op1Swap2 # 1-ary op
# We work in a temporary directory, i.e., delete all generated files on exit.
# For a real experiment, you would put an existing directory path into `td` by
# doing `from pycommons.io.path import Path; td = Path("mydir")` and not use
# the `with` block.
with temp_dir() as td:
run_experiment( # run the JSSP experiment with the following parameters:
base_dir=td, # base directory to write all log files to
algorithms=[ # the set of algorithm generators
lambda inst, pwr: RLS(Op0Shuffle(pwr), Op1Swap2()), # algo 1
lambda inst, pwr: HillClimber(Op0Shuffle(pwr), Op1Swap2())], # 2
instances=("demo", "abz7", "la24"), # we use 3 JSSP instances
max_fes=10000, # we grant 10000 FEs per run
n_runs=4) # perform 4 runs per algorithm * instance combination
end_results = [] # this list will receive the end results records
from_logs(td, end_results.append) # get results from log files
end_stats = [] # the list to receive the statistics records
# compute end result statistics for all algorithm+instance combinations
from_end_results(end_results, end_stats.append)
# store the statistics to a CSV file
es_csv = to_csv(end_stats, td.resolve_inside("end_stats.txt"))
print(es_csv.read_all_str()) # read and print the file
# When leaving "while", the temp directory will be deletedWe will get something like the following output:
# Experiment End Results Statistics
# See the description at the bottom of the file.
algorithm;instance;objective;encoding;n;bestF.min;bestF.mean;bestF.med;bestF.geom;bestF.max;bestF.sd;lastImprovementFE.min;lastImprovementFE.mean;lastImprovementFE.med;lastImprovementFE.geom;lastImprovementFE.max;lastImprovementFE.sd;lastImprovementTimeMillis.min;lastImprovementTimeMillis.mean;lastImprovementTimeMillis.med;lastImprovementTimeMillis.geom;lastImprovementTimeMillis.max;lastImprovementTimeMillis.sd;totalFEs.min;totalFEs.mean;totalFEs.med;totalFEs.geom;totalFEs.max;totalFEs.sd;totalTimeMillis.min;totalTimeMillis.mean;totalTimeMillis.med;totalTimeMillis.geom;totalTimeMillis.max;totalTimeMillis.sd;goalF;bestFscaled.min;bestFscaled.mean;bestFscaled.med;bestFscaled.geom;bestFscaled.max;bestFscaled.sd;successN;successFEs.min;successFEs.mean;successFEs.med;successFEs.geom;successFEs.max;successFEs.sd;successTimeMillis;ertFEs;ertTimeMillis;maxFEs;maxTimeMillis
hc_swap2;abz7;makespan;operation_based_encoding;4;804;823.5;820;823.3222584158909;850;19.82422760159901;3798;5839.5;5612.5;5556.776850879124;8335;2102.5303010103485;26;57;54;51.55696256128031;94;28.2724836781867;10000;10000;10000;10000;10000;0;68;92.5;95;90.55441161416107;112;21.486429825977762;656;1.225609756097561;1.2553353658536586;1.25;1.2550644183169068;1.295731707317073;0.030219859148778932;0;;;;;;;;inf;inf;10000;300000
hc_swap2;demo;makespan;operation_based_encoding;4;180;192.5;192.5;192.22373987227797;205;11.902380714238083;4;49.75;33.5;27.53060177455133;128;53.98996820397903;1;1.25;1;1.189207115002721;2;0.5;34;7508.5;10000;2414.736402766418;10000;4983;1;62.75;76;26.889958060259907;98;45.78482281280556;180;1;1.0694444444444444;1.0694444444444444;1.0679096659571;1.1388888888888888;0.0661243373013227;1;34;34;34;34;34;;1;30034;251;10000;300000
hc_swap2;la24;makespan;operation_based_encoding;4;1065;1131.75;1114.5;1130.1006812239552;1233;71.47668617575012;2130;4235.25;2471.5;3364.07316907124;9868;3759.9463981108383;14;36;25;28.82037873718377;80;29.888682361946525;10000;10000;10000;10000;10000;0;60;73.5;75.5;72.89589968499726;83;10.661457061146317;935;1.13903743315508;1.210427807486631;1.1919786096256684;1.2086638301860484;1.3187165775401068;0.07644565366390384;0;;;;;;;;inf;inf;10000;300000
rls_swap2;abz7;makespan;operation_based_encoding;4;756;761.5;761.5;761.4899866748019;767;4.509249752822894;8005;9182.75;9395.5;9151.751195919433;9935;853.7393727986702;62;94.25;100.5;91.66752533729615;114;24.005207768315607;10000;10000;10000;10000;10000;0;68;102.75;114;100.40278492339303;115;23.18584338197197;656;1.1524390243902438;1.1608231707317074;1.1608231707317074;1.1608079065164663;1.1692073170731707;0.006873856330522731;0;;;;;;;;inf;inf;10000;300000
rls_swap2;demo;makespan;operation_based_encoding;4;180;180;180;180;180;0;33;65.75;73;61.7025293022418;84;23.879907872519105;1;1;1;1;1;0;33;65.75;73;61.7025293022418;84;23.879907872519105;1;1;1;1;1;0;180;1;1;1;1;1;0;4;33;65.75;73;61.7025293022418;84;23.879907872519105;1;65.75;1;10000;300000
rls_swap2;la24;makespan;operation_based_encoding;4;1015;1026.25;1028.5;1026.2261982741852;1033;8.05708797684788;5218;7821.5;8308.5;7620.464638595248;9451;1932.6562894972642;32;62;61.5;57.75986004802567;93;25.468935326524086;10000;10000;10000;10000;10000;0;58;76.25;72.5;74.35251132261814;102;20.039544239661073;935;1.085561497326203;1.0975935828877006;1.1;1.0975681264964547;1.1048128342245989;0.008617206392350722;0;;;;;;;;inf;inf;10000;300000
# This file provides statistics about the end results of multiple runs of optimization algorithms on optimization problems.
...
The moptipy system offers a set of tools to evaluate the results collected from experiments.
On one hand, you can export the data to formats that can be processed by other tools.
On the other hand, you can plot a variety of different diagrams.
These diagrams can then be stored in different formats, such as svg (for the web) or pdf (for scientific papers).
We already discussed two formats that can be used to export data to Excel or other software tools.
The End Results CSV format produces semicolon-separated-values files that include the states of each run.
For every single run, there will be a row with the algorithm name, instance name, and random seed, as well as the best objective value, the last improvement time and FE, and the total time and consumed FEs.
It is possible to select "virtual" limits for the runtime (measured in either FEs or milliseconds) and the objective value and to obtain the end results of the algorithms if these were the termination criteria.
This is, of course, only possible if we logged algorithm progress (i.e., did at least set_log_improvements(True)) over runtime and if these virtual limits are less or equal to the actual termination criteria.
The End Results Statistics CSV format allows you to export statistics aggregated, e.g., over the instance-algorithm combinations, for instance over all algorithms, or for one algorithm over all instances. The format is otherwise similar to the End Results CSV format.
We also support converting our experimental results to the IOHprofiler data format.
This can be done by the function moptipy_to_ioh_analyzer, which accepts a source directory in the moptipy structure and a path to a destination folder where the IOHprofiler-formatted data will be stored.
You can then analyze it with the IOHanalyzer.
If you have the moptipy package installed, then you can call the module directly from the command line as:
python3 -m moptipy.evaluation.ioh_analyzer source_dir dest_dirwhere source_dir should be the root directory with the experimental data (see Section 5.1.1)) and dest_dir is the directory where the IOHprofiler-formatted data should be written.
In the file examples/progress_plot.py, you can find some code running a small experiment and creating "progress plots." A progress plot is a diagram that shows how an algorithm improves the solution quality over time. The solution quality can be the raw objective value, the objective value scaled by the goal objective value, or the objective value normalized with the goal objective value. The time can be measured in objective function evaluations (FEs) or in milliseconds and may be log-scaled or unscaled. A progress plot can illustrate groups of single runs that were performed in the experiments. It can also illustrate statistics over the runs, say, the arithmetic mean of the best-so-far objective value at a given point in time. Both types of data can also be combined in the same diagram.
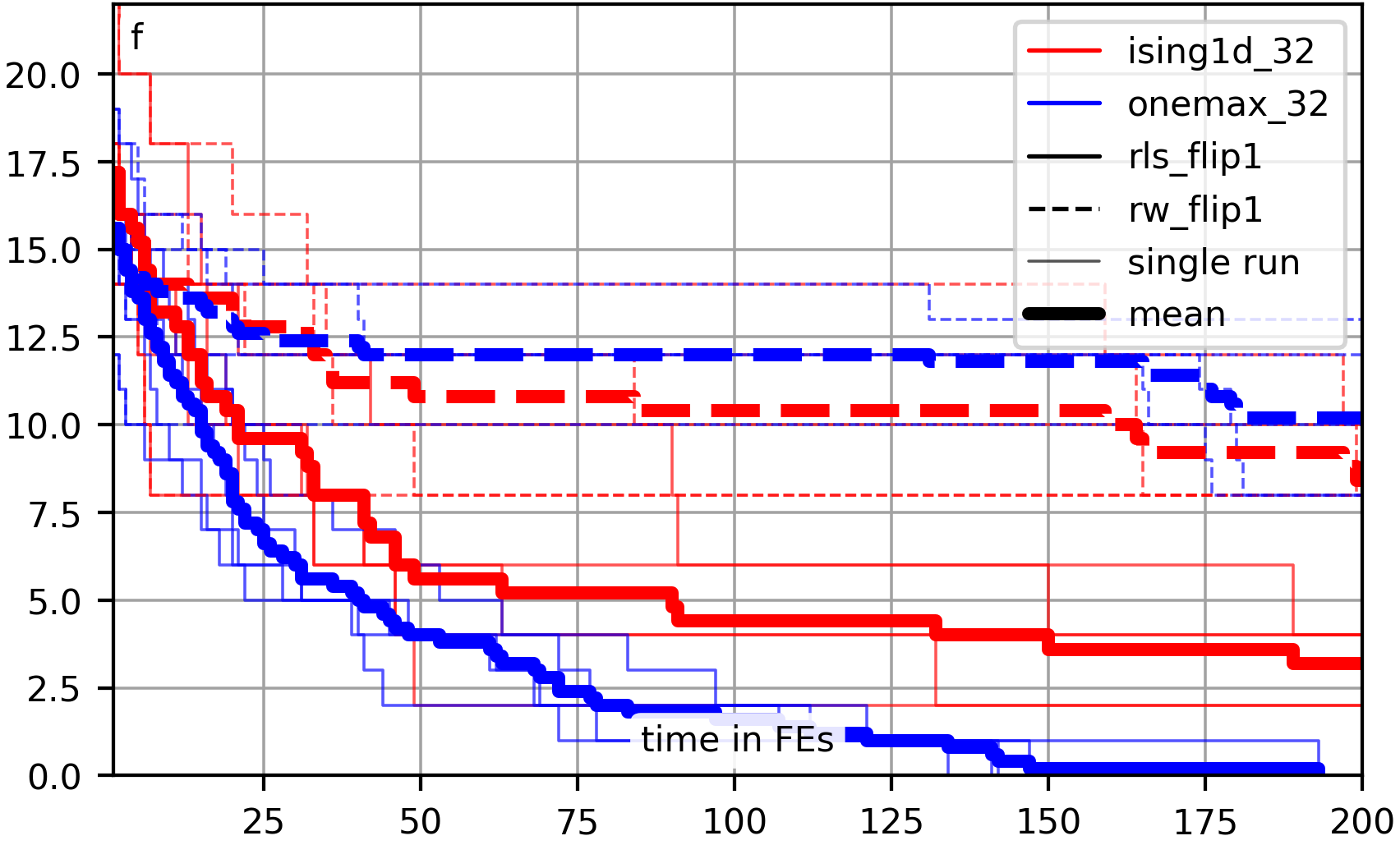
Progress plots are implemented in the module moptipy.evaluation.plot_progress.
In the file examples/end_results_plot.py, you can find some code running a small experiment and creating "end results plots." An end results plot is basically a box plot overlay on top of a violin plot.
Imagine that you conduct multiple runs of one algorithm on one problem instance, let's say 50. Then you get 50 log files and each of them contains the best solution discovered by the corresponding run. Now you may want to know how the corresponding 50 objective values are distributed. You want to get a visual impression about this distribution. Our end results diagram provide this impression by combining two visualizations:
The box plot in the foreground shows the
- the median
- the 25% and 75% quantile
- the 95% confidence interval around the median (as notch)
- the arithmetic mean (as a triangle symbol)
- whiskers at the 5% and 95% quantiles, and
- the outliers on both ends of the spectrum.
The violin plot in the background tries to show the approximate distribution of the values. A violin plot is something like a smoothed-out, vertical, and mirror-symmetric histogram. Whereas you can see and compare statistical properties of the end result distribution from the box plots, you cannot really see how they are actually distributed. For example, it is not clear if the distribution is uni-modal or multi-modal. You can see this from the violins plotted in the background.
If you compute such plots over multiple algorithm-instance combinations, data will automatically be grouped by problem instance. This means that the violin-boxes of different algorithms on the same problem will be plotted next to each other. This, in turn, allows you to easily compare algorithm performance.
In order to make comparing algorithm performance over different instances easier, this plot will use scaled objective values by default.
It will use the goal objective values g from the log files to scale all objective values f to f/g.
Ofcourse you can also use it to plot raw objective values, or even runtimes if you wish.
In the file end_results_with_limits_plot.py, you can find an example of the interplay of this type of plots with the "virtual" runtime limits that can be specified when parsing moptipy.evaluation.end_results.EndResults.
Here, we run an RLS on three OneMax instances for 126 FEs per run.
We then plot the result distribution that we get after 16, 32, 64, and 128 FEs in different charts inside one figure.
It can be seen nicely how the end result distribution approaches 0, i.e., the optimum, more and more everytime we double runtime.
All plots are generated from the same source data, which is possible since we log all the improvements during the runs.
We can know what results we would be getting if we only gave 16 FEs since we know the complete progress up to 128 FEs.
The end result plots are implemented in the module moptipy.evaluation.plot_end_results.
In the file examples/ecdf_plot.py, you can find some code running a small experiment and creating "ECDF plots."
The Empirical Cumulative Distribution Function (ECDF) is a plot that aggregates data over several runs of an optimization algorithm.
It has the consumed runtime (in FEs or milliseconds) on its horizontal axis and the fraction of runs that succeeded in reaching a specified goal on its vertical axis.
Therefore, an ECDF curve is a monotonously increasing curve:
It remains 0 until the very first (fastest) run of the algorithm reaches the goal, say at time T1.
Then, it will increase a bit every single time another run reaches the goal.
At the point in time T2 when the slowest, last run reaches the goal, it becomes 1.
Of course, if not all runs reach the goal, it can also remain at a some other level in [0,1].
Let's say we execute 10 runs of our algorithm on a problem instance.
The ECDF remains 0 until the first run reaches the goal.
At this time, it would rise to value 1/10=0.1.
Once the second run reaches the goal, it will climb to 2/10=0.2.
If 7 out of our 10 runs can solve the problem and 3 fail to do so, the ECDF would climb to 7/10=0.7 and then remain there.
ECDF plots are implemented in the module moptipy.evaluation.plot_ecdf.
In the file examples/ert_plot.py, you can find some code running a small experiment and creating empirically estimated Expected Running Time (ERT) plots.
Basically, it illustrates an estimation of the runtime that it would take in expectation to reach certain objective values.
The objective values are therefore printed on the horizontal axis and the vertical axis associates an expected running time to them.
This expectation is estimated based on the idea of iterated runs:
Assume that you conduct an experiment with 100 runs.
Now you want to know how long your algorithm needs in expectation to reach a certain goal quality f.
However, you are unlucky:
Only 30 of your runs actually reached f, the rest of them converged to a worse solution and stopped improving before being finally terminated.
To compute the ERT, we simply assume that if a run did not succeed, we would have directly restarted our algorithm and performed a new, independent run right away.
Each time we start a run, the chance to succeed is 30% as 30 of our 100 runs managed to find a solution with a quality no worse than f.
We would do this until we finally succeed.
This means that as long as at least one of our runs succeeded in the experiment, we can compute a finite ERT.
For any goal f, the ERT is computed as
ERT[f] = Time(fbest >= f) / s
where s is the number of successful runs, i.e., of runs that reached the goal f and Time(fbest >= f) is the sum of the runtime of all runs that was spent until the objective value reached f (or the run terminated).
Equipped with this understanding, we can now compute the ERT for every single objective value that was reached by any of our runs. This way, we will get a diagram similar to the one below:
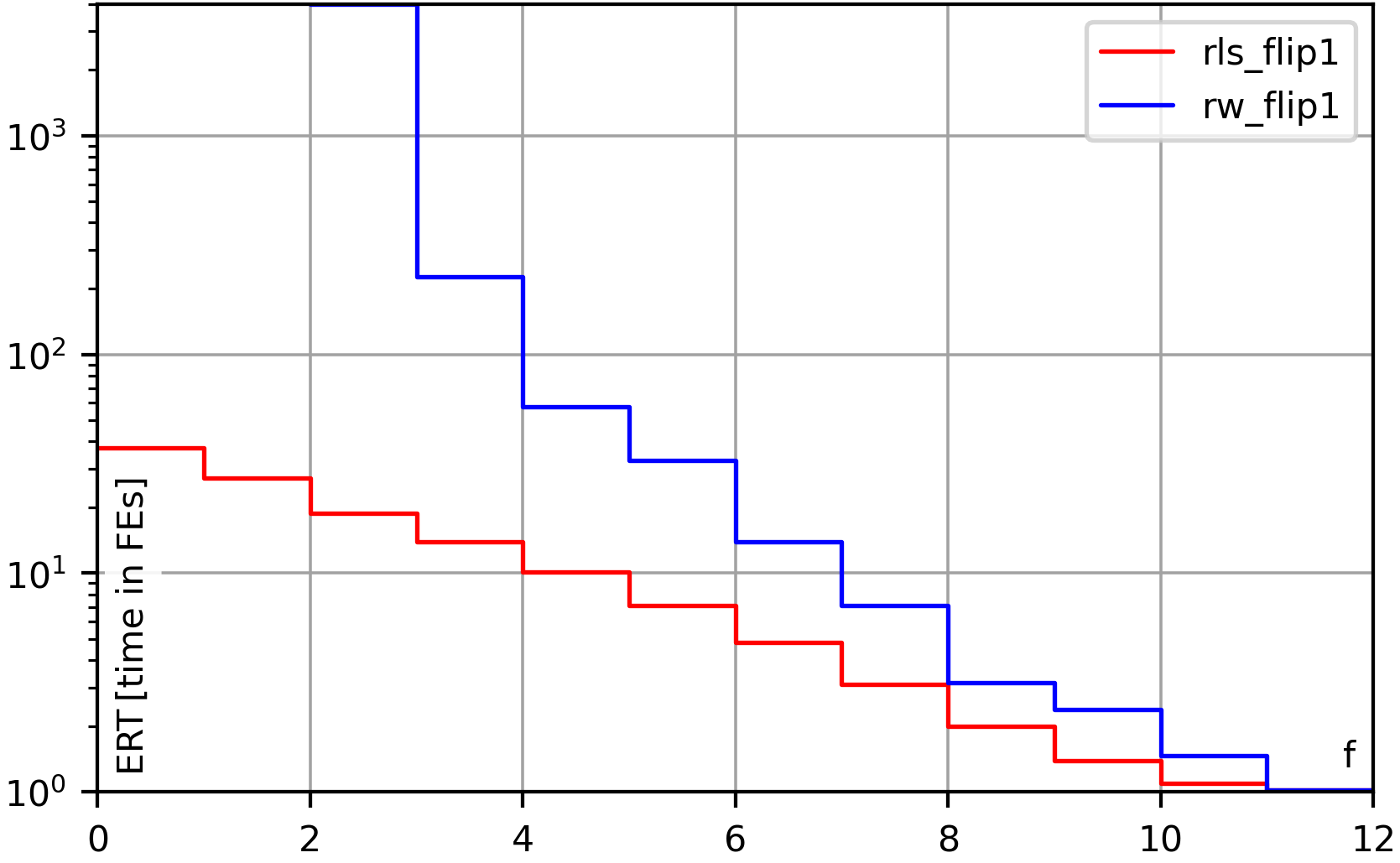
The (empirically estimated) Expected Running Time (ERT) is nicely explained in the report Real-Parameter Black-Box Optimization Benchmarking 2010: Experimental Setup. The ERT plots are implemented in the module moptipy.evaluation.plot_ert.
In the file examples/ertecdf_plot.py, you can find some code running a small experiment and creating ERT-ECDF plots. These plots combine the concepts of ERTs with ECDFs: Their vertical axis shows the fraction of problem instances that can be expected to be solved by an algorithm. Their horizontal axis shows the runtime consumed to do so, which is equivalent to the ERT of the algorithm to reach the global optimum. While ECDFs themselves are based on single runs, ERT-ECDF plots are based on problem instances. They also make the same assumptions as ERTs, namely that we can simply restart an algorithm if it was not successful when it had consumed all of its computational budget. Like ECDF-plots, the ERT-ECDF plots are implemented in the module moptipy.evaluation.plot_ecdf.
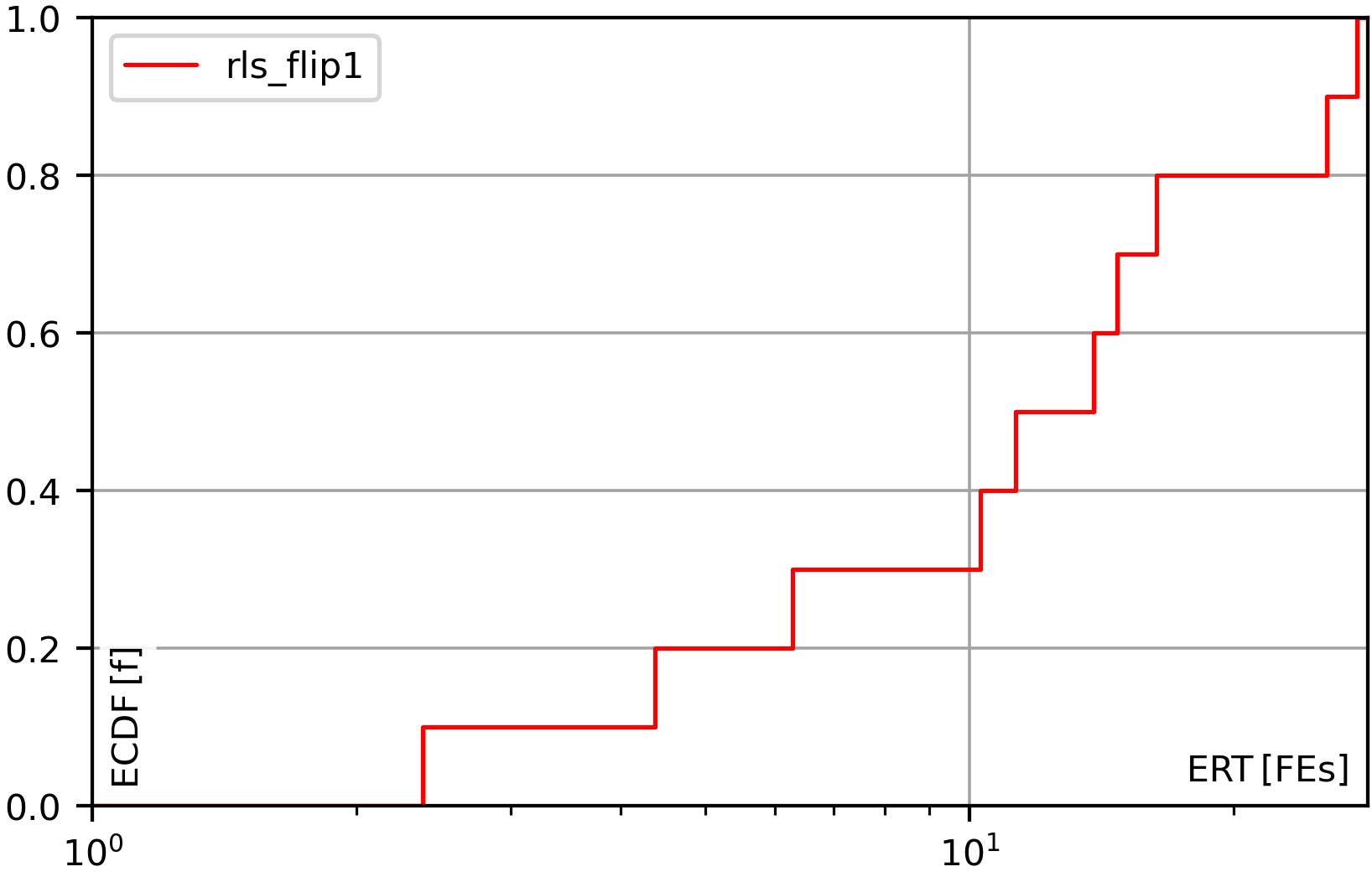
Often we want to investigate how and algorithm parameter or an instance feature impacts the algorithm performance. The function plot_end_statistics_over_param can do both:
In examples/end_statistics_over_feature_plot.py, it is used to visualize the ERT of a simple RLS algorithm over the instance size n of the OneMax problem.
Basically, the minimization version of the OneMax problem tries to minimize the number of 0s in a bit string of length n.
Of course, the higher n, the longer it will take to solve the problem.
We apply the RLS several times to the instances of sizes n in 1..20.
We then load the end results and convert them to end result statistics.
All we need to tell our system how it can deduce the value of the feature from an EndStatistics and which statistic we want to plot (here: ertFEs) and we are good:
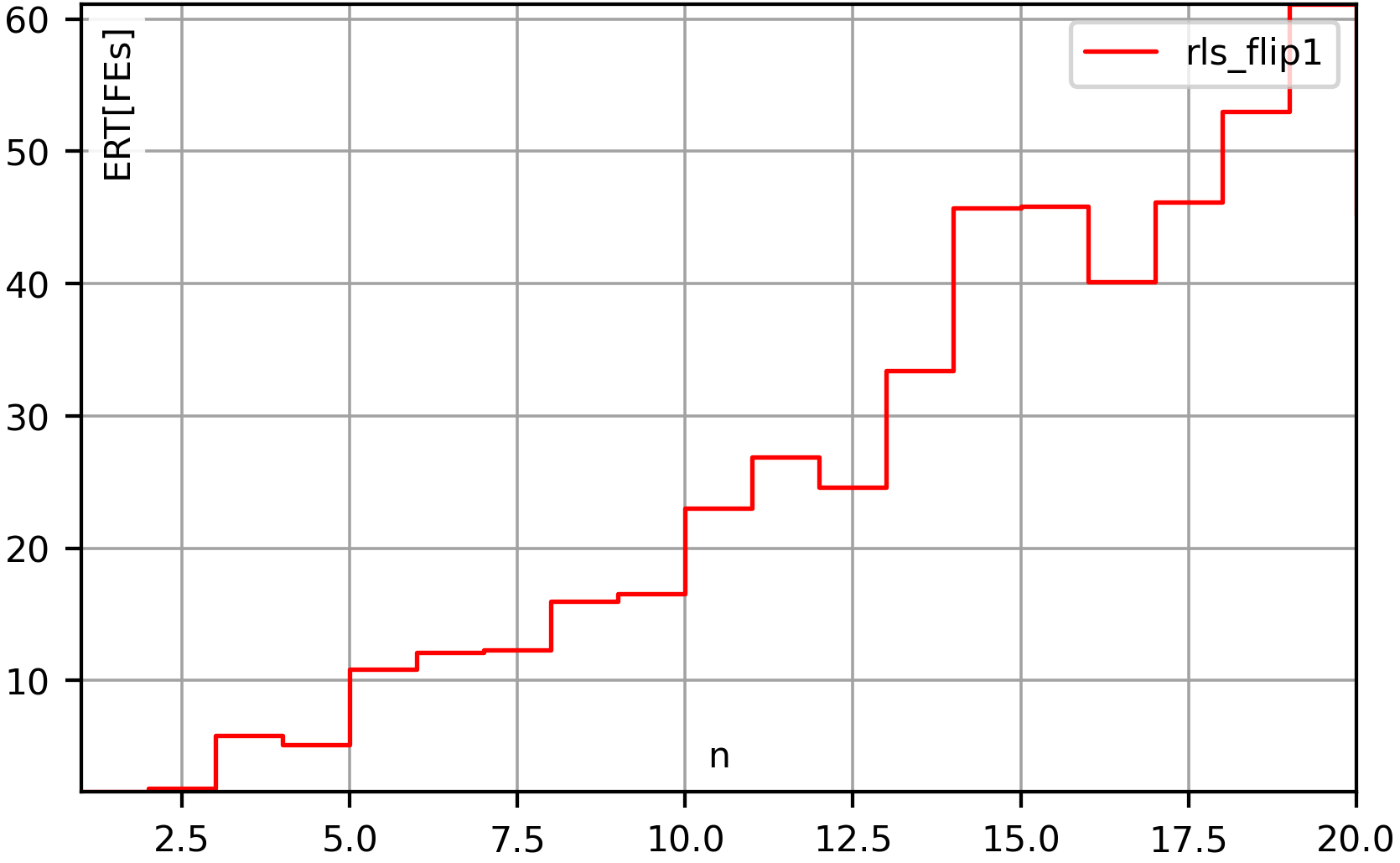
In examples/end_statistics_over_param_plot.py, on the other hand, we apply the same method to analyze the impact of an algorithm parameter on the performance.
We again apply an RLS algorithm algorithm, but this time with a configurable operator, Op1MoverNflip, which flips each bit in a string with a probability distributed according to Bin(m/n), where n is the total number of bits and m is a parameter.
We apply this algorithm for different values of m to two instances of the minimization version of the LeadingOnes problem.
We plot the mean end result after 128 FEs (on the vertical axis) over the values of m (horizontal axis).
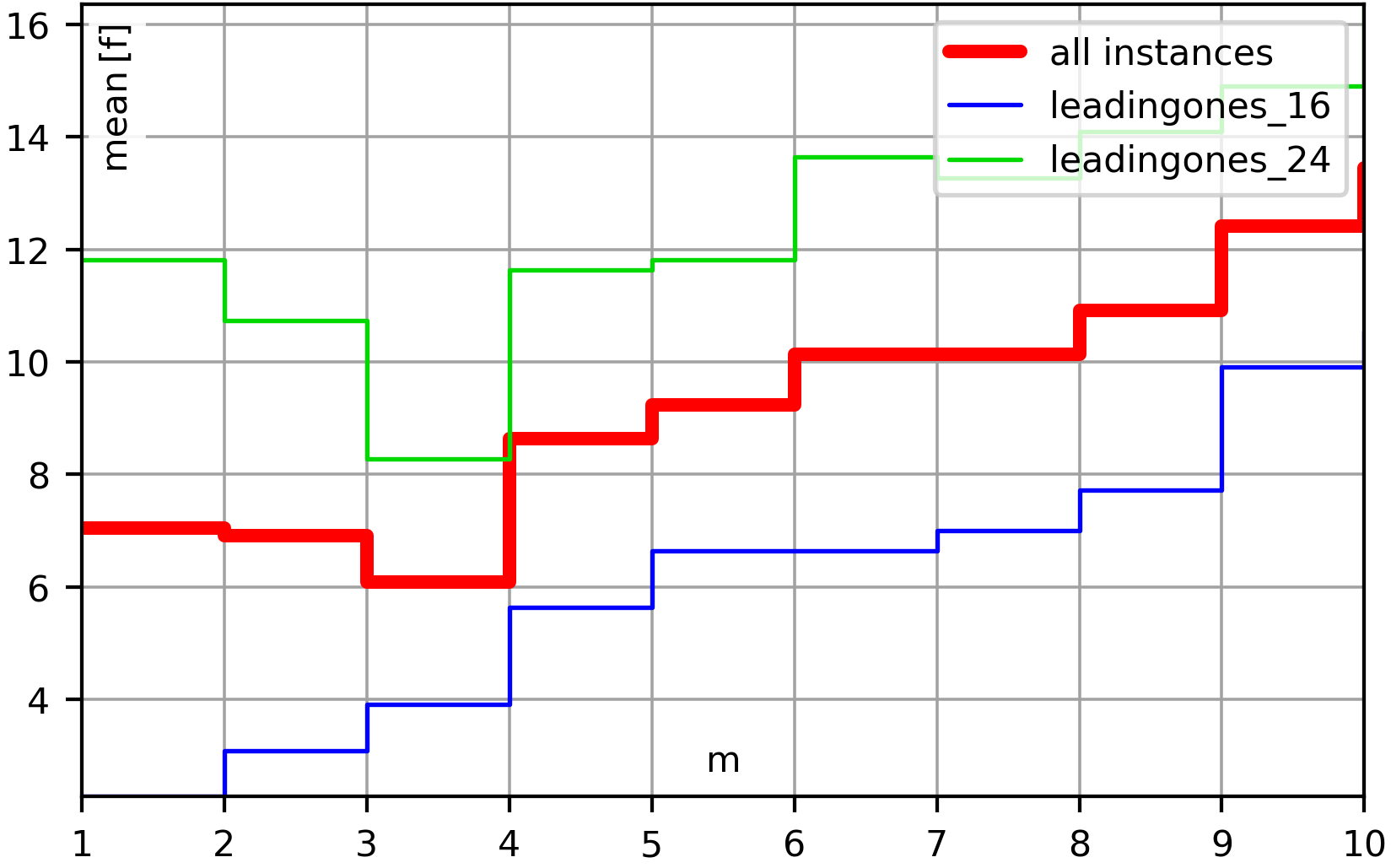
These plots have been implemented in the module moptipy.evaluation.plot_end_statistics_over_parameter.
In the file examples/end_results_table.py, you can find some code running a small experiment and creating an "end results table." Such a table allows you to display statistics summarizing the performance of your algorithms over several problem instances. In their standard configuration, they two parts:
- Part 1 displays information about the algorithm-instance combinations.
For each instance, it has one row per algorithm.
This row displays, by default, the following information about the performance of the algorithm on the instance, aggregated over all runs:
I: the instance namelb(f): the lower bound of the objective value of the instancesetup: the name of the algorithm or algorithm setupbest: the best objective value reached by any run on that instancemean: the arithmetic mean of the best objective values reached over all runssd: the standard deviation of the best objective values reached over all runsmean1: the arithmetic mean of the best objective values reached over all runs, divided by the lower bound (or goal objective value)mean(fes): the arithmetic mean of the index of the last objective function evaluation (FE) which resulted in an improvement, over all runsmean(t): the arithmetic mean of the time in milliseconds when the last improving move of a run was applied, over all runs
- The second part of the table presents one row for each algorithm with statistics aggregated over all runs on all instances.
By default, it holds the following information:
setup: the name of the algorithm or algorithm setupbest1: the minimum of the best objective values reached divided by the lower bound (or goal objective value) over all runsgmean1: the geometric mean of the best objective values reached divided by the lower bound (or goal objective value) over all runsworst1: the maximum of the best objective values reached divided by the lower bound (or goal objective value) over all runssd1: the standard deviation of the best objective values reached divided by the lower bound (or goal objective value) over all runsmean(fes): the arithmetic mean of the index of the last objective function evaluation (FE) which resulted in an improvement, over all runsmean(t): the arithmetic mean of the time in milliseconds when the last improving move of a run was applied, over all runs
For each column of each group (instances in part 1, the complete part 2), the best values are marked in bold face.
Tables can be rendered to different formats, such as Markdown, LaTeX, and HTML. The example examples/end_results_table.py, for instance, produces the following Markdown table:
| I | lb(f) | setup | best | mean | sd | mean1 | mean(fes) | mean(t) |
|---|---|---|---|---|---|---|---|---|
dmu23 |
4'668 | hc_swap2 |
6'260 | 6'413.6 | 191.78 | 1.374 | 626 | 10 |
rls_swap2 |
5'886 | 6'177.7 | 164.08 | 1.323 | 704 | 11 | ||
rs |
7'378 | 7'576.6 | 122.78 | 1.623 | 357 | 8 | ||
ft06 |
55 | hc_swap2 |
57 | 59.3 | 1.25 | 1.078 | 133 | 2 |
rls_swap2 |
55 | 57.0 | 1.91 | 1.036 | 333 | 4 | ||
rs |
60 | 60.4 | 0.79 | 1.099 | 651 | 5 | ||
la24 |
935 | hc_swap2 |
1'122 | 1'180.7 | 61.74 | 1.263 | 752 | 9 |
rls_swap2 |
1'078 | 1'143.0 | 48.23 | 1.222 | 752 | 10 | ||
rs |
1'375 | 1'404.3 | 26.66 | 1.502 | 248 | 3 | ||
| setup | best1 | gmean1 | worst1 | sd1 | mean(fes) | mean(t) | ||
| summary | hc_swap2 |
1.036 | 1.231 | 1.444 | 0.1 | 504 | 7 | |
| summary | rls_swap2 |
1.000 | 1.187 | 1.377 | 0.1 | 596 | 8 | |
| summary | rs |
1.091 | 1.389 | 1.650 | 0.2 | 419 | 5 |
It also produces the same table in LaTeX:
\begin{tabular}{lrlrrrrrr}%
\hline%
I&lb(f)&setup&best&mean&sd&mean1&mean(fes)&mean(t)\\%
\hline%
{\texttt{dmu23}}&4'668&{\texttt{hc\_swap2}}&6'260&6'413.6&191.78&1.374&626&10\\%
&&{\texttt{rls\_swap2}}&{\textbf{5'886}}&{\textbf{6'177.7}}&164.08&{\textbf{1.323}}&{\textbf{704}}&{\textbf{11}}\\%
&&{\texttt{rs}}&7'378&7'576.6&{\textbf{122.78}}&1.623&357&8\\%
\hline%
{\texttt{ft06}}&55&{\texttt{hc\_swap2}}&57&59.3&1.25&1.078&133&2\\%
&&{\texttt{rls\_swap2}}&{\textbf{55}}&{\textbf{57.0}}&1.91&{\textbf{1.036}}&333&4\\%
&&{\texttt{rs}}&60&60.4&{\textbf{0.79}}&1.099&{\textbf{651}}&{\textbf{5}}\\%
\hline%
{\texttt{la24}}&935&{\texttt{hc\_swap2}}&1'122&1'180.7&61.74&1.263&{\textbf{752}}&9\\%
&&{\texttt{rls\_swap2}}&{\textbf{1'078}}&{\textbf{1'143.0}}&48.23&{\textbf{1.222}}&752&{\textbf{10}}\\%
&&{\texttt{rs}}&1'375&1'404.3&{\textbf{26.66}}&1.502&248&3\\%
\hline%
&&setup&best1&gmean1&worst1&sd1&mean(fes)&mean(t)\\%
\hline%
summary&&{\texttt{hc\_swap2}}&1.036&1.231&1.444&0.1&504&7\\%
summary&&{\texttt{rls\_swap2}}&{\textbf{1.000}}&{\textbf{1.187}}&{\textbf{1.377}}&{\textbf{0.1}}&{\textbf{596}}&{\textbf{8}}\\%
summary&&{\texttt{rs}}&1.091&1.389&1.650&0.2&419&5\\%
\hline%
\end{tabular}%The end result tables are implemented in the module moptipy.evaluation.tabulate_end_results.
In the file examples/end_results_tests.py, you can find some code running a small experiment and creating a table of statistical end result tests. In such a table, a set of algorithms is compared pairwise on a set of problem instances using the two-tailed Mann-Whitney U test with the Bonferroni correction.
The output in markdown of the table generated in examples/end_results_tests.py looks as follows:
| Mann-Whitney U |
rls_flip1 vs. rls_flipB1
|
rls_flip1 vs. rls_flipB2
|
rls_flipB1 vs. rls_flipB2
|
|---|---|---|---|
leadingones_100 |
9.286*10^-2^ ?
|
8.820*10^-5^ >
|
3.746*10^-3^ ?
|
leadingones_200 |
— | 1.078*10^-2^ ?
|
2.713*10^-2^ ?
|
onemax_100 |
4.343*10^-4^ <
|
5.307*10^-7^ <
|
8.539*10^-3^ ?
|
onemax_200 |
2.096*10^-5^ <
|
2.463*10^-7^ <
|
1.783*10^-3^ ?
|
trap_100 |
2.035*10^-6^ <
|
2.813*10^-8^ <
|
1.250*10^-4^ <
|
trap_200 |
2.627*10^-3^ ?
|
1.649*10^-6^ <
|
2.453*10^-3^ ?
|
< / ? / >
|
3/3/0 | 4/1/1 | 1/5/0 |
As you can see, we compare three algorithms, rls_flip1, rls_flipB1, and rls_flipB2, on six problem instances, the 100 and 200 bit versions of the LeadingOnes, OneMax, and Trap, problems.
For each algorithm pair on each instance, a two-sided Mann-Whitey U test is applied.
This test computes the probability p that the observed difference in performance (here: end result qualities) of the two compared algorithms would occur if the two algorithms would perform exactly the same.
In other words, if p is high, the chance that any apparent difference in performance just stems from randomness is high.
If one algorithm was better than the other and p is sufficiently small, then be confident that it truly is better.
We therefore define a significance threshold alpha, an upper limit for p that we deem acceptable.
In other words, alpha is the limit for the probability to be wrong when claiming that one algorithm is better than the other that we are going to accept.
Since we perform multiple test, alpha'=alpha/n_tests is computed, i.e., the Bonferroni correction is applied.
We use alpha' as actual threshold to ensure that the probability that any of our n_tests statements is wrong is <=alpha.
The first column of the table contains the problem instances.
Each other column holds the p value, together with the signs <, ?, and <.
-< means that the performance metric of the first algorithm had both smaller mean and median values compared to the second algorithm and p<alpha'.
>means that the performance metric of the first algorithm had both larger mean and median values compared to the second algorithm andp<alpha'.?means that, while one of the two algorithms had a smaller mean and median value,p>=alpha', i.e., the observed difference was not significant.- A cell with a dash (—) inside denotes that the two compared algorithms either had the same mean and median performance, or one was better in mean and the other was better in median. Even if we would conduct a statistical test, it would be meaningless to claim that either of the two algorithms was better.
The bottom row of the table sums up the numbers of <, ?, and > outcomes for each algorithm pair.
The end result comparison tables are implemented in the module moptipy.evaluation.tabulate_result_tests.
Here we list the set of examples that are provided in the moptipy repository in the folder "examples".
- continuous_optimization.py applies a set of numerical/continuous optimization algorithms to a simple problem and prints their results.
- continuous_optimization_with_logging.py is exactly the same example, but this time log files are created and their contents are printed for each run.
- ecdf_plot.py runs a small experiment on the
OneMaxproblem and plots the ECDF. - end_results_jssp.py runs a small experiment with on the Job Shop Scheduling Problem (JSSP) and generates an end results CSV file.
- end_results_plot.py applies two algorithms to the JSSP and creates plots of end results.
- end_results_table.py runs another small experiment on the JSSP and generates a table of end results.
- end_results_tests.py runs a small experiment on bit string search spaces and generates a table with statistical comprisons of end results.
- end_results_with_limits_plot.py runs a small experiment with one algorithm on three
OneMaxinstances and collects the whole algorithm progress in the log files. It then plots plots of end results for different runtime limits. - end_statistics_jssp.py runs a small experiment on the JSSP and generates an end statistics CSV file.
- end_statistics_over_feature_plot.py solves several
OneMaxinstances and plots the ERT over the problem scale, i.e., generates a performance-over-feature plot. - end_statistics_over_param_plot.py applies different settings of an algorithm to LeadingOnes instances and plots their performance over their parameter setting.
- ert_plot.py applies an algorithm to the
OneMaxand plots the ERT over the solution qualities. - ertecdf_plot.py applies one algorithm to several
OneMaxinstances and creates an ERT-ECDF plot. - experiment_2_algorithms_4_problems.py shows how to use the structured experiment API and applies two algorithms to four problem instances (
OneMaxand LeadingOnes). - experiment_own_algorithm_and_problem.py shows how to implement some of the core components of our API, namely how a self-implemented algorithm can be applied to a self-implemented problem.
- log_file_jssp.py showcases the log file structure for single-objective optimization.
- mo_example.py is a simple example for multi-objective optimization: we apply multi-objective RLS to a multi-objective version of the JSSP.
- mo_example_nsga2.py the same simple example for multi-objective optimization, but this time using the popular NSGA-II algorithm, which works out better than our multi-objective RLS.
- mo_example_nsga2_bits.py another example of NSGA-II solving a multi-objective optimization problem, this time over the space of the bit strings.
- The package
moptipy.examples.jsspcontains a complete experiment on the Job Shop Scheduling Problem (JSSP) together with its evaluation routines, making up an epxerimental part of the book "Optimization Algorithms". - progress_plot.py shows how progress plots can be generated from a small experiment with the
OneMaxproblem and the 1-dimensional Ising model. - single_run_rls_onemax.py shows how we can perform a single run of a single algorithm on a single problem instance.
When developing and applying randomized algorithms, proper testing and checking of the source code is of utmost importance. If we apply a randomized metaheuristic to an optimization problem, then we usually do not which solution quality we can achieve. Therefore, we can usually not know whether we have implemented the algorithm correctly. In other words, detecting bugs is very hard. Unfortunately, this holds also for the components of the algorithms, such as the search operators, especially if they are randomized as well. A bug may lead to worse results and we might not even notice that the worse result quality is caused by the bug. We may think that the algorithm is just not working well on the problem.
Therefore, we need to test all components of the algorithm as far as we can. We can try check, for example, if a randomized nullary search operator indeed creates different solutions when invoked several times. We can try to check whether an algorithm fails with an exception. We can try to check whether the search operators create valid solutions and whether the algorithm passes valid solutions to the objective function. We can try to whether an objective function produces finite objective values and if bounds are specified for the objective values, we can check whether they indeed fall within these bounds. Now we cannot prove that there are no such bugs, due to the randomization. But by testing a few hundred times, we can at least detect very obvious and pathological bugs.
To ease such testing for you, we provide a set of tools for testing implemented algorithms, spaces, and operators in the package moptipy.tests. Here, you can find functions where you pass in instances of your implemented components and they are checked for compliance with the moptipy API. In other words, if you go and implement your own algorithms, operators, and optimization problems, you can use our pre-defined unit tests to give them a thorough check before using them in production. Again, such tests cannot prove the absence of bugs. But they can at least give you a fair shot to detect pathological errors before wasting serious experimentation time.
We also try to extensively test our own code, see the coverage report.
Examples for the variety of testing tools provided are:
validate_componentchecks whether an object is a validmoptipycomponent (which is the base class of allmoptipyobjects). It tests whether the conversion to string yields a valid name without invalid characters and whether logging of the component parameters works.validate_algorithmfirst checks if an algorithm is validmoptipycomponent and then applies it to a (user-provided) example problem. It checks whether this works without exception, whether the computational budget is used correctly, and whether any inconsistencies in the final solution can be detected.validate_mo_algorithmis the multi-objective version ofvalidate_algorithm.validate_objectivechecks whether an objective function is implemented consistently, i.e., if its upper and lower bound are valid, if the result of evaluating some random solutions falls within these bounds, if it really only returns integers if it claims to do so, if it returns the same objective value for the same solution, and so on.validate_encodingchecks whether an encoding is implemented consistently.validate_op0,validate_op1, andvalidate_op2check whether nullary, unary, and binary operators are implemented consistently, respectively.validate_spacechecks whether an object is a consistent implementation of amoptipySpace.
There are also a set of pre-defined objectives, encodings, and spaces that can be used as shortcuts so that you do not need to specify them manually for the different validate_* routines.
You can test elements on
- bit string-based problems,
- permutation-based problems, or on
- the JSSP
Another way to try to improve and maintain code quality is to use static code analysis and type hints where possible and reasonable. A static analysis tool can inform you about, e.g., unused variables, which often result from a coding error. It can tell you if the types of expressions do not match, which usually indicates a coding error, too. It can tell you if you perform some security-wise unsafe operations (which is less often a problem in optimization, but it does not hurt to check). Code analysis tools can also help you to enforce best practices, which are good for performance, readability, and maintainability. They can push you to properly format and document your code, which, too, improve readability, maintainability, and usability. They even can detect a set of well-known and frequently-occurring bugs. We therefore also run a variety of such tools on our code base, including (in alphabetical order):
autoflake, a tool for finding unused imports and variablesbandit, a linter for finding security issuesdodgy, for checking for dodgy looking values in the codeflake8, a collection of lintersflake8-bugbear, for finding common bugsflake8-eradicate, for finding commented-out codeflake8-use-fstring, for checking the correct use of f-stringsmypy, for checking types and type annotationspycodestyle, for checking the formatting and coding style of the sourcepydocstyle, for checking the format of the docstringspyflakes, for detecting some errors in the codepylint, another static analysis toolpyroma, for checking whether the code complies with various best practicesruff, a static analysis tool checking a wide range of coding conventionssemgrep, another static analyzer for finding bugs and problemstryceratops, for checking against exception handling anti-patternsunimport, for checking against unused import statementsvulture, for finding dead code
On git pushes, GitHub also automatically runs CodeQL to check for common vulnerabilities and coding errors. We also turned on GitHub's private vulnerability reporting and the Dependabot vulnerability and security alerts.
Using all of these tools increases the build time. However, combined with thorough unit testing and documentation, it should help to prevent bugs, to improve readability, maintainability, and usability of the code. It does not matter whether we are doing research or try to solve practical problems in the industry — we should always strive to make good software with high code quality.
Often, researchers in particular think that hacking something together that works is enough, that documentation is unimportant, that code style best practices can be ignored, and so on. And then they wonder why they cannot understand their own code a few years down the line (at least, this happened to me in the past…). Or why no one can use their code to build atop of their research (which is the normal case for me).
Improving code quality can never come later.
We always must maintain high coding and documentation standards from the very beginning.
While moptipy may still be far from achieving these goals, at least we try to get there.
Anyway, you can find our full make build running all the tests, doing all the static analyses, creating the documentation, and creating and packaging the distribution files here.
Besides the basic moptipy dependencies, it requires a set of additional dependencies.
These are all automatically installed during the build procedure.
The build only works under Linux.
Experiments with moptipy are reproducible and repeatable (according to the ACM definition) if the results are recorded in log files.
As stated in the log files section, our log files should store all the information relevant to a single run of an optimization algorithm.
First, the log files can store the complete algorithm setups and objective function information as well as the involved fully-qualified class names.
They also store the system configuration, which includes the versions of the libraries used.
This should allow to re-create algorithm setups and system configuration.
Each run of the optimization algorithms on every problem instance is provided with a seeded random number generator via process.get_random().
This must be the only source of randomness used in the algorithms.
In other words, every algorithm must be deterministic and make the same decisions on the same problem instance with the same sequence of random numbers provided by this generator.
The random seed using the generator as well as the numpy classes of the generator and the numpy version are all stored in the log files.
The random seed for a new run can be set via the Execution builder object.
Therefore, if a given algorithm configuration can be re-created on a known instance, it can be started with the same random seed as a known run.
Since the version information and classes of all involved libraries in the random number generation are stored as well, the same random number sequences can be reproduced.
The solutions found by the algorithms are also stored in the log files. Therefore, it is also possible to re-evaluate and verify them as well.
Additionally, if the experiment API is used, then the random seeds are determined based on the instance names.
This means that all algorithms will use the same seeds for each instance, while different problem instances will lead to different seeds.
This, in turn, means that the algorithms start with the same first random solutions (if they use the same nullary operator).
It also means that if you run the same experiment program twice, the same random seeds will be used automatically.
In other words, if you have the complete code of a moptipy compliant experiment, it should (re)produce the exactly same runs with the exactly same results.
Experiments can be parallelized based on runs, where one run is the application of one algorithm to one problem instance.
While each run is still executed sequentially, multiple runs can be executed in parallel.
For executing experiments, the method run_experiment from module moptipy.api.experiment is used, as explained in Section 3.2.
It creates the log file and folder structure discussed in Section 5.1.1. in a replicable way.
This means that if you run the method twice, it would create exactly the same experiment with exactly the same file and folder names.
Since the file and folder structure is repeatable, run_experiment will simply skip all runs that are associated with log files which already exist.
Before doing a run, the system will create the corresponding (empty) log file.
This means that you could launch the experiment program twice in parallel.
Each process would then do about half of the runs, because it will skip the runs for which the log files have been created by the other process.
(It also means that if your experiment crashes, you can simply delete all zero-sized files and start again to continue it.)
You can achieve distributed experiment executing by simply sharing the folder for the log files between the machines. If you use a shared root folder for experiments and launch the same experiment on multiple machines, they will automatically distribute the work load amongst each other using this very (and therefore very robust) simple system.
- Our project can be found on GitHub at https://github.com/thomasWeise/moptipy/
- The documentation of our project is available at https://thomasweise.github.io/moptipy/.
- Our project can be found on PyPi at https://pypi.org/project/moptipy/
- Our project can be found on Libraries.io at https://libraries.io/pypi/moptipy, however, this page usually does not show the most recent version.
- Our project can be found on snyk.io at https://snyk.io/advisor/python/moptipy, however, this page usually does not show the most recent version.
- An example data set of experimental results obtained with
moptipycan be found at https://thomasweise.github.io/oa_data/.
- Our book on optimization algorithms, which is currently work in progress: Thomas Weise. Optimization Algorithms. Institute of Applied Optimization (应用优化研究所, IAO) of the School of Artificial Intelligence and Big Data (人工智能与大数据学院) at Hefei University (合肥学院) in Hefei, Anhui, China (中国安徽省合肥市).
- Our old book optimization algorithms: Thomas Weise. Global Optimization Algorithms - Theory and Application.
- The website of our Institute of Applied Optimization (应用优化研究所, IAO) of the School of Artificial Intelligence and Big Data (人工智能与大数据学院) at Hefei University (合肥学院) is http://iao.hfuu.edu.cn.
Here we provide a very incomplete list of other Python software packages that can be used for solving optimization problems (in alphabetical order). A much better list maintained by Keivan Tafakkori can be found here.
cmaesprovides implementations of Covariance Matrix Adaptation Evolution Strategies for solving continuous optimization problems. It is maintained by Masashi Shibata and Masahiro Nomura and available at https://pypi.org/project/cmaes/ and https://github.com/CyberAgent/cmaes. We wrap several of the algorithms into ourmoptipyAPI in modulemoptipy.algorithms.so.vector.cmaes_lib.deapis a novel evolutionary computation framework for rapid prototyping and testing of ideas by Félix-Antoine Fortin, François-Michel De Rainville, Marc-André Gardner, Marc Parizeau, and Christian Gagné. It offers a rich set of evolutionary computation-based metaheuristics and a straightforward API. You can find it on GitHub at https://github.com/DEAP/deap.inspyredandecspyare open source packages for nature-inspired optimization by Aaron Garrett.nevergradby Facebook Research offers gradient free optimization and implements a variety of numerical optimization methods and many benchmark problems.- The library "Powell's Derivative-Free Optimization solvers" (
pdfo) provides an implementation of the "Bound Optimization BY Quadratic Approximation" algorithm, or BOBYQA for short, for solving continuous optimization problems. The library is dedicated to the late Professor M. J. D. Powell FRS (1936—2015), maintained by Tom M. Ragonneau and Zaikun Zhang, and available at https://github.com/pdfo/pdfo and https://www.pdfo.net. We wrap itsBOBYQAimplementation into ourmoptipyAPI in modulealgorithms.so.vector.pdfo. pgapyby Ralf Schlatterbeck provides a Python wrapper the PGAPack Parallel Genetic Algorithm Library. It can be found on GitHub at https://github.com/schlatterbeck/pgapy.scipyoffers a set of well-established mathematical optimization techniques for continuous optimization via the functionscipy.optimize.minimize. We wrap some of them into ourmoptipyAPI in modulealgorithms.so.vector.scipy.
- The IOHprofiler is a nice piece of open source software for analyzing the performance of optimization algorithms.
It is possible to convert our
moptipylog data to the format understood by the IOHanalyzer, which allows you to use this software to analyze your optimization results as well. You can then upload the data to the online IOHanalyzer service and evaluate it. - A nice discussion of experimentation with (numerical) optimization methods is: Nikolaus Hansen, Anne Auger, Steffen Finck, Raymond Ros. Real-Parameter Black-Box Optimization Benchmarking 2010: Experimental Setup. Research Report RR-7215, INRIA. 2010. inria-00462481
- Thomas Weise and Zhize Wu. 2023. Replicable Self-Documenting Experiments with Arbitrary Search Spaces and Algorithms. In Genetic and Evolutionary Computation Conference Companion (GECCO'23 Companion), July 15-19, 2023, Lisbon, Portugal. ACM, New York, NY, USA, 9 pages. doi:10.1145/3583133.3596306. ISBN: 979-8-4007-0120-7.
- Thomas Weise. Optimization Algorithms. 2021-ongoing. https://thomasweise.github.io/oa.
This is a book introducing metaheuristic optimization methods using
moptipyas a source for example implementations and showcase experiments. - Tianyu Liang, Zhize Wu, Jörg Lässig, Daan van den Berg, Thomas Weise. Solving the Traveling Salesperson Problem using Frequency Fitness Assignment. IEEE Symposium on Foundations of Computational Intelligence (IEEE FOCI'22), part of the IEEE Symposium Series on Computational Intelligence (SSCI'22), December 4-7, 2022, Singapore. doi:10.1109/SSCI51031.2022.10022296 This paper investigates Frequency Fitness Assignment (FFA) on the Traveling Salesperson Problem.
- Newsletter of the ACM Special Interest Group on Genetic and Evolutionary Computation. Volume 16, Issue 4, December 2023, Software Category. "motipy: the Metaheuristic Optimization in Python Library" https://sigevo.hosting.acm.org/public_html/sigevolution/2023/12/04/volume-16-issue-4
moptipy is a library for implementing, using, and experimenting with metaheuristic optimization algorithms.
Our project is developed for scientific, educational, and industrial applications.
Copyright (C) 2021-2023 Thomas Weise (汤卫思教授)
Dr. Thomas Weise (see Contact) holds the copyright of this package except for the JSSP instance data in file moptipy/examples/jssp/instances.txt.
moptipy is provided to the public as open source software under the GNU GENERAL PUBLIC LICENSE, Version 3, 29 June 2007.
Terms for other licenses, e.g., for specific industrial applications, can be negotiated with Dr. Thomas Weise (who can be reached via the contact information below).
This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version. This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details. You should have received a copy of the GNU General Public License along with this program. If not, see https://www.gnu.org/licenses/.
Please visit the contributions guidelines for moptipy if you would like to contribute to our package.
If you have any concerns regarding security, please visit our security policy.
If you have any questions or suggestions, please contact Prof. Dr. Thomas Weise (汤卫思教授) of the Institute of Applied Optimization (应用优化研究所, IAO) of the School of Artificial Intelligence and Big Data (人工智能与大数据学院) at Hefei University (合肥大学) in Hefei, Anhui, China (中国安徽省合肥市) via email to [email protected] with CC to [email protected].

